Python实现:汉诺塔问题
汉诺塔问题不管在任何编程语言里都是经典问题,是采用递归算法的经典案例,该问题可以抽象如下:
一 、3根圆柱A,B,C,其中A上面串了n个圆盘
二 、这些圆盘从上到下是按从小到大顺序排列的,大的圆盘任何时刻不得位于小的圆盘上面
三 、每次移动一个圆盘,最终实现将所有圆盘移动到C上
利用Python语言接近自然语言的特性,开发者可以更容易的将递归算法翻译成程序语句,需要的代码量很小。汉诺塔问题的解决步骤用语言描述很简单,仅三步:
A,B,C三个圆柱,分别为初始位,过渡位,目标位,设A柱为初始位,C位为最终目标位
(1)将最上面的n-1个圆盘从初始位移动到过渡位
(2)将初始位的最底下的一个圆盘移动到目标位
(3)将过渡位的n-1个圆盘移动到目标位
对于递归算法中的嵌套函数f(n-1)来说,其初始位,过渡位,目标位发生了变化
代码如下:
import turtle class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items) def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2] def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates def pole_stack():#制造poles的栈
poles=[Stack() for i in range(3)]
return poles def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-1)*400,-90+20*l) def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole) myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()
运行结果:
输入需要演示的汉诺塔层数并回车,这次我试的是5。(层数越多,动画演示时间越长)
演示的是动画,我只是截了这个过程的一张图
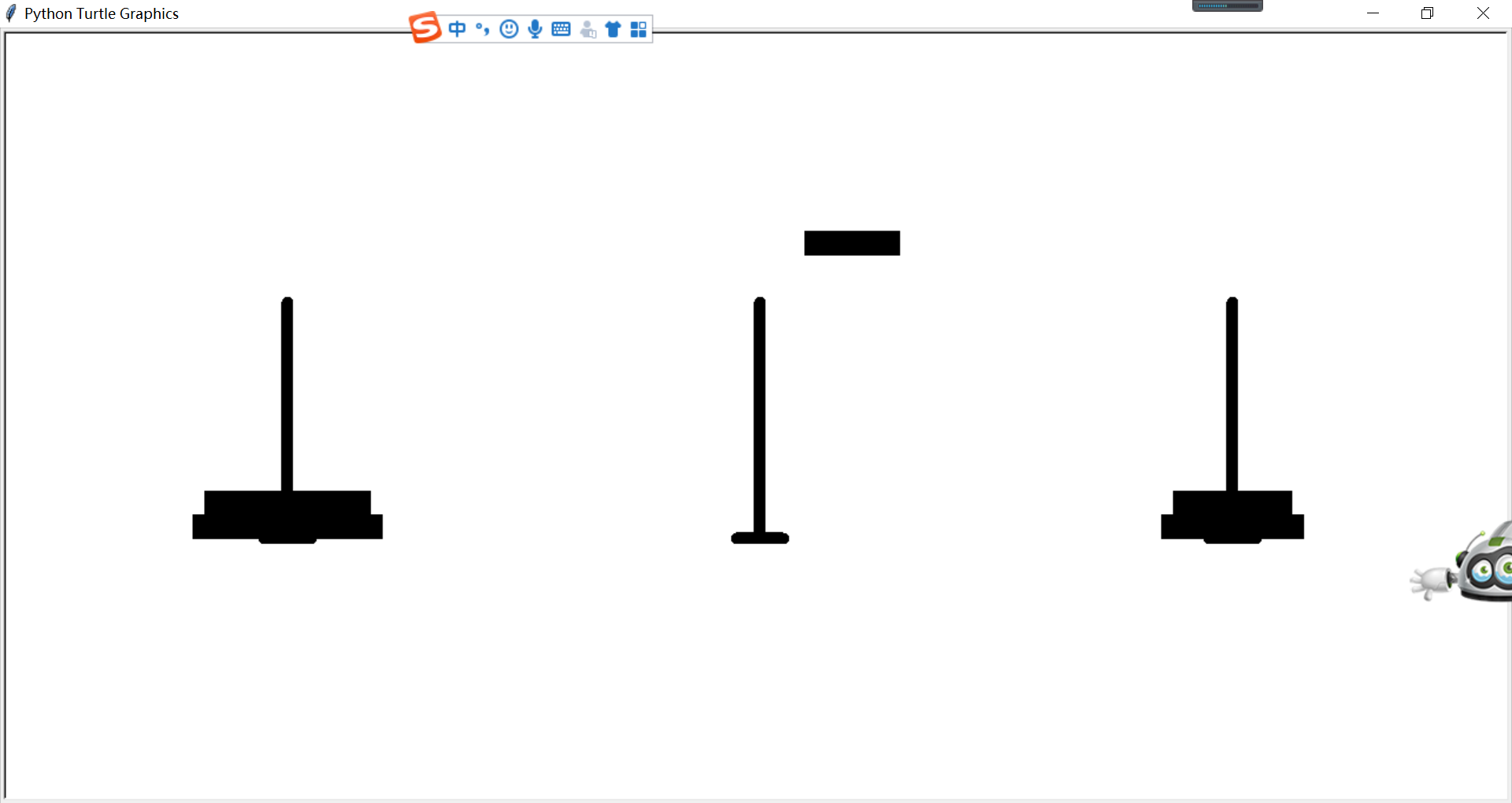
Python实现:汉诺塔问题的更多相关文章
- python 游戏 —— 汉诺塔(Hanoita)
python 游戏 —— 汉诺塔(Hanoita) 一.汉诺塔问题 1. 问题来源 问题源于印度的一个古老传说,大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆 ...
- python解决汉诺塔问题
今天刚刚在博客园安家,不知道写点什么,前两天刚刚学习完python 所以就用python写了一下汉诺塔算法,感觉还行拿出来分享一下 首先看一下描述: from :http://baike.baidu. ...
- 【学习】Python解决汉诺塔问题
参考文章:http://www.cnblogs.com/dmego/p/5965835.html 一句话:学程序不是目的,理解就好:写代码也不是必然,省事最好:拿也好,查也好,解决问题就好! ...
- Python实现汉诺塔问题的可视化(以动画的形式展示移动过程)
学习Python已经有一段时间了,也学习了递归的方法,而能够实践该方法的当然就是汉诺塔问题了,但是这次我们不只是要完成对汉诺塔过程的计算,还要通过turtle库来体现汉诺塔中每一层移动的过程. 一.设 ...
- python递归——汉诺塔
汉诺塔的传说 法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针.印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了 ...
- Python之汉诺塔递归运算
汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆 ...
- python 实现汉诺塔
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺 ...
- python实现汉诺塔
经典递归算法汉诺塔分析: 当A柱子只有1个盘子,直接A --> C 当A柱子上有3个盘子,A上第一个盘子 --> B, A上最后一个盘子 --> C, B上所有盘子(1个) --&g ...
- python实现汉诺塔移动
汉诺塔问题 汉诺塔是根据一个传说形成的一个问题.汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大 ...
- python实现汉诺塔问题
汉诺塔问题可以简单描述成为将a柱子上的圆盘按一定规则借助b柱子完美地复制到c柱子上.现假设有a,b,c三根柱子,a柱子上的圆盘从上到下依次标号为1,2,3,……,n,且为递增状态.规则:每次移动一个盘 ...
随机推荐
- Java基础(进制转换-)
进制概述: 进制也就是进位计数制,是人为定义的带进位的计数方法(有不带进位的计数方法,比如原始的结绳计数法,唱票时常用的“正”字计数法,以及类似的tally mark计数). 对于任何一种进制---X ...
- 基于C#的Appium自动化测试框架(Ⅰ):程序结构
因为工作原因,使用的编程语言都是C#,但是国内相应的Appium资料少得可怜,Java版本的Appium也考虑过,但是奈何自己搞不定Eclipse这个编译环境[说白了就是因为懒…… 无意中看到了外面的 ...
- python迭代器的原理及应用
''''什么是迭代器?迭代的工具1.什么是迭代? 迭代是一个重复的过程,每一次重复都是基于上一次结果而进行的while True: print('hello world')像上面做这种单纯的重复并不是 ...
- 初识JDBC
1,概念: JDBC(Java DateBase Connective) ,即利用Java语言操作数据库语言 2,示例:Mysql中的JDBC 1,新建一个Dynamic Web Projectx项目 ...
- Oracle生成GUID
,),),),),) GUID FROM ( SELECT SYS_GUID() GUID FROM DUAL )
- 对比剖析Swarm Kubernetes Marathon编排引擎
Docker Native Orchestration 基本结构 Docker Engine 1.12 集成了原生的编排引擎,用以替换了之前独立的Docker Swarm项目.Docker原生集群(S ...
- linux随
Linux 1991芬兰大学生linus 安全 开源 免费 可靠 (堡垒机)(跳转机) 多用户 多任务 处理并发及速度比windows好很多 命令:ifconfig pwd ls -a -l -t(时 ...
- ntfs读写工具Paragon NTFS 15无限使用教程
Paragon NTFS mac版是Mac OS平台上最受欢迎的ntfs读写工具,专门开发用来弥补Windows和Mac OS X之间的不兼容性,通过在Mac OS X系统下提供对任何版本的NTFS文 ...
- nginx rewrite (转发)
1.location正则写法 一个示例: location = / { # 精确匹配 / ,主机名后面不能带任何字符串 [ configuration A ] } location / { # 因为所 ...
- 升级python2.7, 实现python2.7与python3并存
由于用到twilio模块, 所以需要升级一下python2, 但是又不想舍弃python2, 于是实现了简单的方法 python 先扔一块依赖 yum install zlib-devel bzip2 ...
