BUAA-OO-表达式解析与求导

解析

按照常规，解析这一部分我们分为词法分析与语法分析。当然由于待解析的字符串较简单，词法分析器和语法分析器不必单独实现。

词法分析器

按照常规，我们先手写一个词法分析器，而不使用正则表达式。

词法分析器：读取字符流，产生标记流。它聚合字符形成单词，并应用一组规则来判断每个单词在源语言中是否合法，如果合法则为其分配一个语法范畴，产生一个标记。

我们的词法分析器行为如下：

如果当前输入有定义，则为其产生一个标记(token, token value)。譬如：当前输入是"+114514"，则为其产生标记(Num, +114514)；当前输入是"*"，则为其产生标记(Op,*)，诸如此类。
如果当前的输入无定义，则抛出错误。譬如：当前输入是"y"，则抛出错误。

可能你已经发现，这个词法分析器并不能很好地满足我们的需求：当输入为"+114514"时，如何判断是"+"，或是"+114514"呢？

这里我们需要额外介绍一个概念：lookahead，即提前看多个字符。由于有一个或多个标记是以相同的字符开头的，仅凭当前的字符无法确定具体应该解释为哪个标记，所以只能再向前查看字符。以"+114514"为例，在解析到"+"之后，还需要向前查看一个字符"1"，此时就能够确定当前输入对应的标记种类应为 Num。

具体实现

完成词法分析器的行为定义之后，我们开始进行更为详尽的设计。

首先，由定义，我们可以得到我们所需的标记种类：

/**
  * Num : 数字
  * Op  : 运算符
  * Sin : Sin函数
  * Cos : Cos函数
  * X   : 幂函数
  * LP  : 左括号
  * RP  : 右括号
  * NULL: 字符流末尾
  */
enum TokenType {
    Num, Op, Sin, Cos, X, LP, RP, NULL
}

接下来就是枯燥的枚举：

void getTok() {
    token="";
    tokenType = TokenType.NULL;
    // consume blank char
    { /* some code */ }
    // reach the end
    { /* some code */ }
    switch (currentCharacter) {
        case 'x' :
            /* some code */
        case 's' :
            /* some code */
        default :
            throw new someKindOfException();
    }

词法分析器部分告一段落。

语法分析器

文法

首先根据定义给出文法

<expr> ::= <expr> + <term>
         | <expr> - <term>
         | <term>
<term> ::= <term> * <factor>
         | <factor>
<factor> ::= (<expr>)
           | Num
           | sin(<factor>)
           ...

在文法中出现了两种符号，一种是被<>包围的非终结符，如<expr>，可以用 ::= 右侧的式子替代；另一种是没有出现在 ::= 左侧的终结符，如 Num，一般对应于词法分析器输出的标记。

解析过程

然后是递归下降的解析过程，关于什么是递归下降，稍后会进行解释。以 1*(2+3) 为例

<expr> => <expr>
        => <term>      * <factor>
         => <factor>      |
          => Num (3)      |
                          => (<expr>)
                           => <expr>       + <term>
                            => <term>         |
                             => <factor>      |
                              => Num (2)      |
                                              => <factor>
                                               => Num (3)

整个解析的过程是在不断对非终结符进行替换（向下），直到遇到了终结符（底）。在解析的过程中，有的非终结符，如<expr>被递归地使用了。

递归下降：从起始非终结符开始，不断地对非终结符进行分解，直到匹配输入的终结符。

可以看出，整个解析的过程和我们的文法是十分相近的，我们可以很容易地将文法直接转换成实际的代码，只需为每个非终结符定义一个对应的函数。不过，很显然我们的文法是没有办法直接翻译成实际代码的，这是编译原理的内容了，此处不再赘述。

除了递归下降以外，还可以选择使用自底向上的方法进行语法分析，由于是手写语法分析器，我们不考虑采用自底向上。

语法树

根据解析过程，我们很自然地会想到树这种数据结构。一个简略的语法树如下

            expr
           /  |  \
        term  term ...
        / | \
     num sin cos ...

具体实现

以下是根据文法直接翻译的一个不可能的实现。

Expr parseExpr() {
    Expr result = new Expr();
    loop {
        // create a node
        Term term = parseTerm();
        // attach
        result.addNode(term);
    }
    return result;
}
Term parseTerm() {
    Term result = new Term();
    loop {
        // create a node
        Factor factor = parseFactor();
        // attach
        result.addNode(factor);
    }
    return result;
}
Factor parseFactor() {
    Factor result = new Factor();
    loop {
        {/* some code */}
    }
    return result;
}

至此，已完成对输入字符串的解析。

求导

根据字符串解析的方法，我们求导的方式也是自顶向下的。

以下是根据语法树得到的一个不可能的实现

Expr exprDiff() {
    Expr result = new Expr();
    for (term : termContainer) {
        result.addNode(termDiff(term));
    }
    return result;
}
Term termDiff() {
    Term result = new Term();
    for (factor : factorContainer) {
        result.addNode()
    }
    return result;
}
Factor factorDiff() {
    return diff();
}

个人实现分析

度量分析

UML类图：

Method Metrics：

Class Metrics：

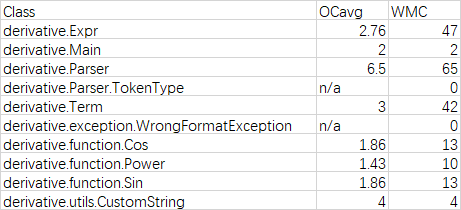
以上为第三次表达式解析与求导作业的UML图和代码指标度量。可以看得出来其中不乏有许多设计和算法问题，譬如

没有另外设置一个Factor的抽象类或者接口，而是将各种Functions直接继承自Expr
模块间的耦合度高，没有合理地设计每个类暴露的接口形状
没有在创建树结点时存储其相应的HASH值，而是在每次进行相等性判断时都进行一次递归运算，大大提高了时间复杂度
在判断相等时用的是简单的遍历比较，而不是设计一个可以避免碰撞的HASH函数

设计模式

简单地运用了工厂模式，将各种Functions的创建托管至Expr。但是这并不是一个好的设计，应该如上述，Expr和各种Functions都继承自Factor抽象类，然后创建一律托管至FactorFactory。否则Functions实现的改变可能会影响Expr实现的改变，这将增大迭代开发和后期维护的复杂度。