2019.2.25考试T1， 矩阵快速幂加速递推+单位根反演（容斥）

\(\color{#0066ff}{题解}\)

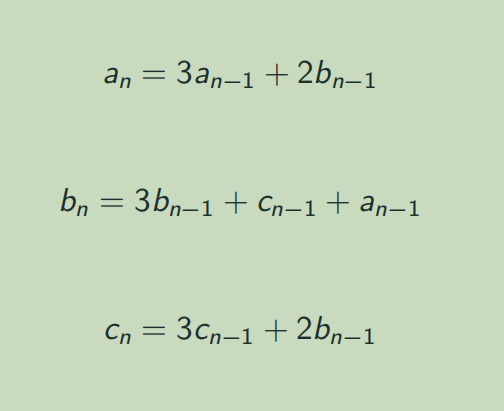
然后a，b，c通过矩阵加速即可

为什么1出现偶数次3没出现的贡献是上面画绿线的部分呢？

考虑暴力统计这部分贡献，答案为\(\begin{aligned}\sum_{2|i}C_n^i*3^{n-i}\end{aligned}\)

显然如果没有\(\sum\)下面的限制，它就是一个生成函数\((x+3)^n\)

相当于我们只取偶数项

可以用单位根反演

把\(\omega_2^1，\omega_2^2\)分别代入\((x+3)^n\)

得到的就是2倍的和，然后再除以2，就是上面绿色部分

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int mod = 1e9 + 7;
const int maxn = 1e6 + 10;
struct node {
	LL ju[3][3];
	node(LL a = 0, LL b = 0, LL c = 0, LL d = 0, LL e = 0, LL f = 0, LL g = 0, LL h = 0, LL i = 0) {
		ju[0][0] = a, ju[0][1] = b, ju[0][2] = c;
		ju[1][0] = d, ju[1][1] = e, ju[1][2] = f;
		ju[2][0] = g, ju[2][1] = h, ju[2][2] = i;
	}
	friend node operator * (const node &a, const node &b) {
		node t;
		for(int i = 0; i < 3; i++)
			for(int j = 0; j < 3; j++)
				for(int k = 0; k < 3; k++)
					(t.ju[i][j] += a.ju[i][k] * b.ju[k][j] % mod) %= mod;
		return t;
	}
	node ksm(LL b) {
		node re(1, 0, 0, 0, 1, 0, 0, 0, 1);
		node a = *this;
		while(b) {
			if(b & 1) re = re * a;
			a = a * a;
			b >>= 1;
		}
		return re;
	}
};
LL ksm(LL x, LL y) {
	LL re = 1LL;
	while(y) {
		if(y & 1) re = re * x % mod;
		x = x * x % mod;
		y >>= 1;
	}
	return re;
}
LL a[maxn], b[maxn], c[maxn], n;
int main() {
	freopen("number.in", "r", stdin);
	freopen("number.out", "w", stdout);
	n = in();
	node A(1), B(3, 1, 0, 2, 3, 2, 0, 1, 3);
	A = A * B.ksm(n);
	LL ans = A.ju[0][0];
	(ans += ksm(3, n)) %= mod;
	LL tot = (ksm(2, n - 1) + (ksm(4, n - 1) << 1LL)) % mod;
	(tot <<= 1LL) %= mod;
	ans = ((ans - tot) % mod + mod) % mod;
	printf("%lld", ans);
	return 0;
}