并不对劲的p2664树上游戏

题目大意

有一棵\(n\)(\(n\leq10^5\))个点的树，每个点\(i\)有颜色\(c_i\)(\(c_i\leq10^5\))

定义一条路径的得分为这条路径上的不同颜色个数

分别求每个点的以该点出发的所有路径的得分总和

题解

统计和路径有关的东西，让人想到点分治

找到当前区域的重心后，计算所有过重心的路径的影响

记每个当前区域里的点\(i\)以重心为根时，当前区域里的子树大小为\(siz_i\)

先分别算出每个颜色\(i\)，对“从重心出发的所有路径的得分总和”的贡献\(W_i\)

发现如果一个点\(i\)的颜色\(c_i\)是从重心到它的路径上第一次出现的，那么它对于每条“以重心为起点，以它子树里的点为终点”的路径都会产生1的贡献，即\(W_{c_i}+=siz_i\)

然后遍历当前区域，对于每种颜色\(i\)，记\(w_i\)表示当前遍历的重心的儿子的子树里，颜色\(i\)对\(W_i\)的贡献为\(w_i\)（也就是说，\(W_i-w_i\)表示颜色\(i\)对“从重心出发的所有不经过当前遍历的重心的儿子路径的得分总和”的贡献）

记\(x\)表示过重心的路径对当前遍历到的点的贡献，初始值为\(\Sigma (W_i-w_i)\)

如果当前点\(i\)的颜色不是在重心到它的路径上第一次出现的，那么\(x\)不变

如果当前点\(i\)的颜色是在重心到它的路径上第一次出现的，\(c_i\)本来只对终点在大小为\(W_{c_i}\)的区域中的路径有贡献，而现在对所有终点不和\(i\)在一个重心的儿子的子树里的路径都有贡献

\(x+=-(W_{c_i}-w_{c_i})+siz_{重心}-siz_{是当前点祖先的重心的儿子}\)

画个图说明一下：

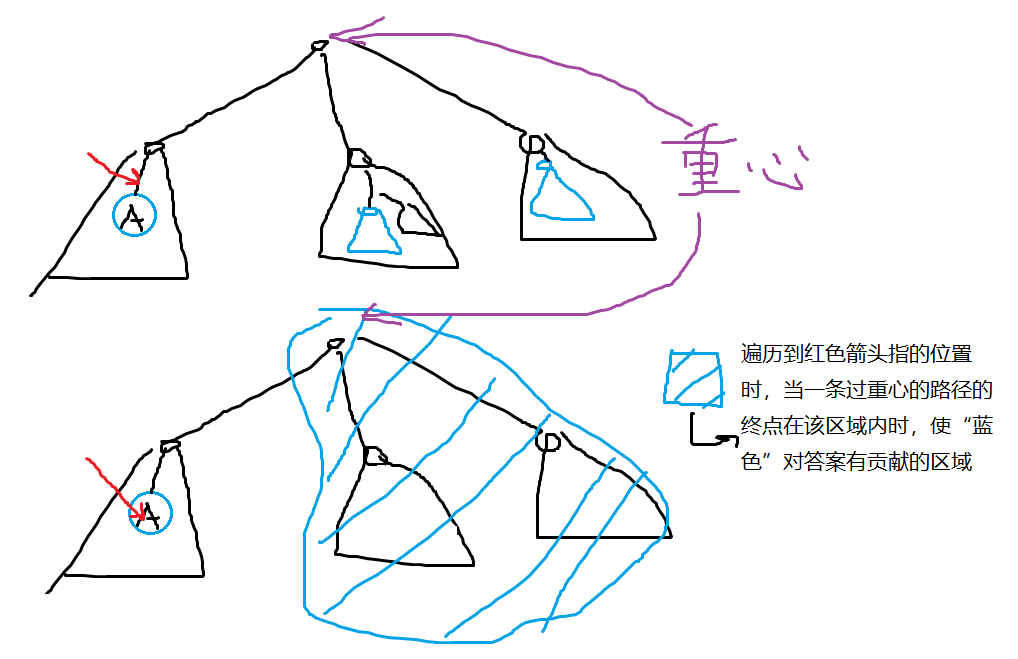
代码

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#include<iomanip>
#include<iostream>
#include<map>
#include<queue>
#include<set>
#include<stack>
#include<vector>
#define rep(i,x,y) for(register int i=(x);i<=(y);++i)
#define dwn(i,x,y) for(register int i=(x);i>=(y);--i)
#define maxn 100010
#define LL long long
#define view(u,k) for(int k=fir[u];k!=-1;k=nxt[k])
using namespace std;
int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)&&ch!='-')ch=getchar();
	if(ch=='-')f=-1,ch=getchar();
	while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
	return x*f;
}
void write(LL x)
{
	if(x==0){putchar('0'),putchar('\n');return;}
	int f=0;char ch[20];
	if(x<0)putchar('-'),x=-x;
	while(x)ch[++f]=x%10+'0',x/=10;
	while(f)putchar(ch[f--]);
	putchar('\n');
	return;
}
int n,c[maxn],fir[maxn],nxt[maxn<<1],v[maxn<<1],siz[maxn],cnt,wt,sumsiz,mnsz,vis[maxn],ext[maxn];
LL sum[maxn],sumall,num[maxn],numnow[maxn],sumnow;
void ade(int u1,int v1){v[cnt]=v1,nxt[cnt]=fir[u1],fir[u1]=cnt++;}
void getwt(int u,int fa)
{
	siz[u]=1;int nowmax=0;
	view(u,k)if(!vis[v[k]]&&v[k]!=fa)getwt(v[k],u),siz[u]+=siz[v[k]],nowmax=max(nowmax,siz[v[k]]);
	if(max(nowmax,sumsiz-siz[u])<mnsz)mnsz=max(nowmax,sumsiz-siz[u]),wt=u;return;
}
void getsz(int u,int fa)
{
	siz[u]=1;
	view(u,k)if(!vis[v[k]]&&v[k]!=fa)getsz(v[k],u),siz[u]+=siz[v[k]];return;
}
void getc(int u,int fa,int f)
{
	int yes=0;
	if(!ext[c[u]])ext[c[u]]=1,yes=1;
	view(u,k)if(!vis[v[k]]&&v[k]!=fa)getc(v[k],u,f);
	if(yes)ext[c[u]]=0,num[c[u]]+=f*siz[u],sumall+=f*siz[u];return;
}
void getnow(int u,int fa,int f)
{
	int yes=0;
	if(!ext[c[u]])ext[c[u]]=1,yes=1;
	view(u,k)if(!vis[v[k]]&&v[k]!=fa)getnow(v[k],u,f);
	if(yes)ext[c[u]]=0,numnow[c[u]]+=f*siz[u],sumnow+=f*siz[u];return;
}
void addsum(int u,int fa,LL ad,LL szanc)
{
	int yes=0;sum[u]+=ad;
	if(!ext[c[u]])yes=1,ext[c[u]]=1,sum[u]+=-(num[c[u]]-numnow[c[u]])+(LL)sumsiz-szanc;
	view(u,k)if(!vis[v[k]]&&v[k]!=fa)addsum(v[k],u,yes?ad-(num[c[u]]-numnow[c[u]])+(LL)sumsiz-szanc:ad,szanc);
	if(yes)ext[c[u]]=0;
}
void getans(int u,int nowsiz)
{
	sumsiz=nowsiz,mnsz=n+1,wt=sumall=0,getwt(u,0);int now=wt;
	getsz(now,0),getc(now,0,1);sum[now]+=sumall;ext[c[now]]=1;
	view(now,k)if(!vis[v[k]])numnow[c[now]]=siz[v[k]],sumnow=siz[v[k]],getnow(v[k],now,1),addsum(v[k],now,sumall-sumnow,siz[v[k]]),getnow(v[k],now,-1),numnow[c[now]]=0;
	ext[c[now]]=0;
	getc(now,0,-1); vis[now]=1;
	view(now,k)if(!vis[v[k]])getans(v[k],siz[v[k]]);return;
}
int main()
{
	n=read();
	memset(fir,-1,sizeof(fir));
	rep(i,1,n)c[i]=read();
	rep(i,1,n-1){int x=read(),y=read();ade(x,y),ade(y,x);}
	getans(1,n);
	rep(i,1,n)write(sum[i]);
	return 0;
}

一些感想

泡狐龙的bgm“妖艶なる舞 〜 タマミツネ”太好听了