√n求单值欧拉函数

基本定理:

首先看一下核心代码：

核心代码

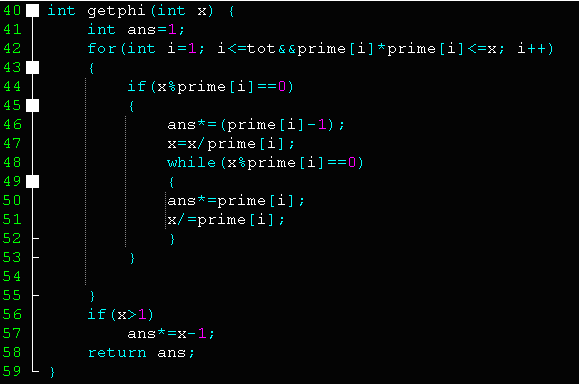
原理解析：

当初我看不懂这段代码，主要有这么几个问题：

1.定理里面不是一开始写了一个n*xxx么？为什么代码里没有*n？

2.ans不是*(prime[i]-1)么？为什么到了第二个while循环变成*prime[i]了？

3.定理里面不是要/pi么？为什么代码里没有/pi?????????????

公式化简

首先我们来分析一下整个程序的原理，如果把程序的原理搞明白了，这三个问题也就自然而然的解决了

这个程序的原理是基于唯一分解定理：

那么我们可以把n拆开，再带回到欧拉函数公式中，然后再约分一下：

LaTex代码：

 ans=p_1^a^*p_2^a^*.......*p_i^a^i*\frac{p_1-}{p_1}*\frac{p_2-}{p_2}*....*\frac{p_i-}{p_i}
    \newline
    =p_1^a^*\frac{p_1-}{p_1}*.......*p_2^a^*\frac{p_2-}{p_2}*....p_i^a^i*\frac{p_i-}{p_i}
    \newline
    =p_1^a^{-}*({p_1-})*.......*p_2^a^{-}*({p_2-})*....p_i^a^{i-}*({p_i-})

解答问题

首先这里的代码实现还有一个小技巧：
我们在while之前把x/prime[i]，这就相当于让ans少*一个prime[i]，这样就可以解决求指数ai-1的问题了

现在再回去看一下刚开始的三个问题，仔细想一想

提示：

下面有答案，

但请认真思考以后再看，

答案在下面：

1.定理里面不是一开始写了一个n*xxx么？为什么代码里没有*n？

因为n被唯一分解了，while循环里面的内容就是用来*n的

2.ans不是*(prime[i]-1)么？为什么到了第二个while循环变成*prime[i]了？

*prime是为了让答案最终*n

3.定理里面不是要/pi么？为什么代码里没有/pi?????????????

被化简了，不明白的可以看上面的化简过程

完整代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const int MAXN=;
 int prime[MAXN];
 int mu[MAXN]= {,};
 int n;
 int tot=;
 int vis[MAXN]= {,};
 void read(int &n) {
     char c='+';
     int x=;
     bool flag=;
     while(c<''||c>'') {
         c=getchar();
         if(c=='-')flag=;
     }
     while(c>=''&&c<='') {
         x=x*+c-;
         c=getchar();
     }
     flag==?n=-x:n=x;
 }
 void ou() {
     for(int i=; i<=n; i++) {
         if(!vis[i])
             prime[++tot]=i,mu[i]=-;
         for(int j=; j<=tot&&j*prime[i]<=n; j++) {
             vis[i*prime[j]]=;
             if((i%prime[j])==) {
                 mu[i*prime[j]]=;
                 break;
             }
             mu[i*prime[j]]=-mu[i];
         }
     }
 }
 int getphi(int x) {
     int ans=;
     for(int i=; i<=tot&&prime[i]*prime[i]<=x; i++)
     {
         if(x%prime[i]==)
         {
             ans*=(prime[i]-);
             x=x/prime[i];
             while(x%prime[i]==)
             {
             ans*=prime[i];
             x/=prime[i];
             }
         }

     }
     if(x>)
         ans*=x-;
     return ans;
 }
 int main() {
     n=;
     ou();
     int c;
     printf("please input the num\n");
     while(cin>>c)
         printf("the num`s phi is %d\n",getphi(c));
     return ;

 }

里面还乱入了线性求莫比乌斯函数的方法，，

懒得删了，，，

结尾啰嗦几句

求单值欧拉函数就讲到这里，

其实对于这份代码还有一种很玄学的理解方法，

但是我的这种方法比较简单易懂，

而且这两种理解方法从本质上来说是一样的

这里不在赘述

最后再说一下，这里只介绍了求单值欧拉函数的方法，

实际上欧拉函数还有线性筛法（因为欧拉函数是积性函数）

有空再介绍吧

另外，因为本人是第一次接触欧拉函数，所以本文肯定有成堆的bug，如果您找出了bug，可以在评论区留言或者通过其他方式联系本人，

谢谢！