已知${a_n}$满足$a_1=1,a_{n+1}=(1+\frac{1}{n^2+n})a_n.$证明:当$n\in N^+$时，

$(1)a_{n+1}>a_n.(2)\frac{2n}{n+1}\le a_n\le \frac{en}{n+1}$

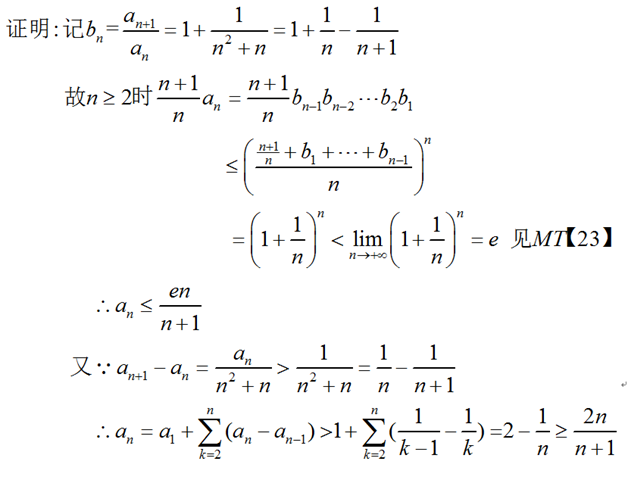
评:当然也可以按参考答案由数学归纳法证明.

MT【71】数列裂项放缩题的更多相关文章

  1. MT【11】对数放缩题

    解答:C 评论:这里讲几个背景知识

  2. MT【167】反复放缩

    已知数列$\{a_n\}$满足:$a_1=1,a_{n+1}=a_n+\dfrac{a_n^2}{n(n+1)}$1)证明:对任意$n\in N^+,a_n<5$2)证明:不存在$M\le4$, ...

  3. MT【170】裂项相消

    已知$a,b>0$证明:$\dfrac{1}{a+2b}+\dfrac{1}{a+4b}+\dfrac{1}{a+6b}<\dfrac{3}{\sqrt{(a+b)(a+7b)}}$ 证明 ...

  4. Problem D: 程序填充（递归函数）：数列2项和

    Problem D: 程序填充(递归函数):数列2项和 Time Limit: 1 Sec  Memory Limit: 64 MBSubmit: 2601  Solved: 2117 Descrip ...

  5. 数列分块入门九题（二）：LOJ6280~6282

    Preface 个人感觉这中间的三题是最水的没有之一 数列分块入门 4--区间加法,区间求和 这个也是很多数据结构完爆的题目线段树入门题,但是练分块我们就要写吗 修改还是与之前类似,只不过我们要维护每 ...

  6. 数列分块入门九题（三）：LOJ6283~6285

    Preface 最后一题我一直觉得用莫队是最好的. 数列分块入门 7--区间乘法,区间加法,单点询问 还是很简单的吧,比起数列分块入门 7就多了个区间乘. 类似于线段树,由于乘法的优先级高于加法,因此 ...

  7. 数列分块入门九题（一）：LOJ6277~6279

    Preface 分块,一个神奇的暴力算法.可以把很多\(O(n^2)\)的数据结构题的暴力优化到常数极小的\(O(n\sqrt n)\).当一些毒瘤题无法用线段树,主席树,平衡树,树状数组...... ...

  8. MT【198】连乘积放缩

    (2018中科大自招最后一题)设$a_1=1,a_{n+1}=\left(1+\dfrac{1}{n}\right)^3(n+a_n)$证明:(1)$a_n=n^3\left(1+\sum\limit ...

  9. 计蒜客 28319.Interesting Integers-类似斐波那契数列-递推思维题 (Benelux Algorithm Programming Contest 2014 Final ACM-ICPC Asia Training League 暑假第一阶段第二场 I)

    I. Interesting Integers 传送门 应该是叫思维题吧,反正敲一下脑壳才知道自己哪里写错了.要敢于暴力. 这个题的题意就是给你一个数,让你逆推出递推的最开始的两个数(假设一开始的两个 ...

随机推荐

  1. sql语句常用功能（null值转换为0）

    COALESCE(规格,' ') 或者 COALESCE(规格,0) select * from ( ) 客户,() 物料号,p4.name 内部批次,p4.outsidename 外部批次,p1.库 ...

  2. LinqPad的变量比较功能

    LinqPad是一个非常方便的C#工具(有免费版和收费版). 今天发现它的变量比较功能真是方便啊.且看3行代码产生如下结果: 说明:图中两个变量的成员属性值分别用红色和绿色背景标注:图很长,只截取了一 ...

  3. bitcoin 源码解析 - 交易 Transaction(二) - 原理篇

    这篇文章我断断续续写了呃···· 应该快三个星期了? 所以前后的风格可能差别相当大.真是十分的怠惰啊··· 最近实在是不够努力.用python重写bitcoin的项目也卡在网络编程部分(这方面真是我的 ...

  4. Linux常用命令行

    实时查看日志runtime.log最后100行 tail -f -n 100 runtime.log

  5. JVM规范系列第6章：Java虚拟机指令集

    一条 Java 虚拟机指令由一个特定操作的操作码和零至多个操作所使用到的操作数所构成. 虚拟机指令 = 操作码 + 操作数. 其中,操作码值分别为 254(0xfe)和 255(0xff),助记符分别 ...

  6. Tomcat通过Redis实现session共享的完整部署记录

    对于生产环境有了一定规模的tomcat集群业务来说,要实现session会话共享,比较稳妥的方式就是使用数据库持久化session.为什么要持久化session(共享session)呢?因为在客户端每 ...

  7. Centos下堡垒机Jumpserver V3.0环境部署完整记录（1）-安装篇

    由于来源身份不明.越权操作.密码泄露.数据被窃.违规操作等因素都可能会使运营的业务系统面临严重威胁,一旦发生事故,如果不能快速定位事故原因,运维人员往往就会背黑锅.几种常见的运维人员背黑锅场景:1)由 ...

  8. 【ML】Two-Stream Convolutional Networks for Action Recognition in Videos

    Two-Stream Convolutional Networks for Action Recognition in Videos & Towards Good Practices for ...

  9. Linux内核及分析 第三周 Linux内核的启动过程

    实验过程: 打开shell终端,执行以下命令: cd LinuxKernel/ qemu -kernel linux-3.18.6/arch/x86/boot/bzImage-initrd rootf ...

  10. ASP.NET MVC使用ADO.NET连接数据库

    深入理解ADO.NET友情链接:http://www.cnblogs.com/liuhaorain/category/352388.html 小白手把手:VS2017  SQL Server 2014 ...