向量的卷积(convolution)运算

一、向量的卷积运算

---

给定两个n维向量α=(a₀, a₁, ..., a_n-1)^T，β=(b₀, b₁, ..., b_n-1)^T，则α与β的卷积运算定义为：

α*β=(c₀, c₁, ..., c_2n-2)^T，其中

事实上，“卷积”的含义从矩阵αβ^T的表示即可以看出：不难发现，c_k即为第k列副对角线元素之和。形象地讲，对α与β作卷积，就像是将由α与β的元素形成的下述矩阵“面”沿副对角线方向卷了起来得到的“一束”向量。

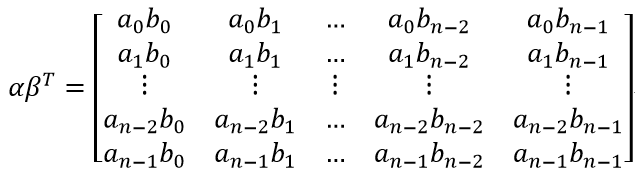
卷积的蛮力算法的时间复杂度为O(n²)。为提高算法效率，可以采用分治策略，这将在下一篇博文有关快速傅立叶变换的内容中予以介绍。

二、卷积应用

---

2.1 多项式乘法

卷积运算与多项式乘法是对应的。不难验证，设多项式f(x)=a₀+a₁x+a₂x²+...+a_m-1x^m-1, g(x)=b₀+b₁x+b₂x²+...+b_n-1x^n-1，则f(x)g(x)得到的多项式的系数列向量就刚好是对f(x)与g(x)的系数列向量的卷积运算的结果。

2.2 信号平滑处理

由于噪声干扰，信号往往需要进行平滑处理。

设信号向量为α=(a₀, a₁, ..., a_m-1)，权向量β=(b_2k, b_2k-1, ..., b₀)=(w_-k, ..., w_k)。一个比较常用的权向量的例子是高斯滤波权值向量，其中

这里z用于归一化处理。

运用权向量β与信号向量α的卷积，我们可以实现为信号去噪，得到向量γ=(a'₀, a'₁, ..., a'_m-1)，其中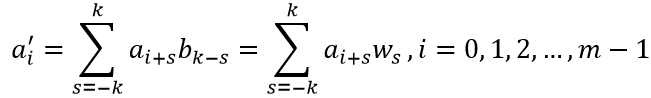

不过，对于边界上的元素，由于缺项无法对齐，经过运算后可能存在误差。