poj 3368 Frequent values -Sparse-Table

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 16537		Accepted: 5981

Description

You are given a sequence of n integers a₁ , a₂ , ... , a_n in non-decreasing order. In addition to that, you are given several queries consisting of indices i and j (1 ≤ i ≤ j ≤ n). For each query, determine the most frequent value among the integers a_i , ... , a_j.

Input

The input consists of several test cases. Each test case starts with a line containing two integers n and q (1 ≤ n, q ≤ 100000). The next line contains n integers a₁ , ... , a_n (-100000 ≤ a_i ≤ 100000, for each i ∈ {1, ..., n}) separated by spaces. You can assume that for each i ∈ {1, ..., n-1}: a_i ≤ a_i+1. The following q lines contain one query each, consisting of two integers i and j (1 ≤ i ≤ j ≤ n), which indicate the boundary indices for the
query.

The last test case is followed by a line containing a single 0.

Output

For each query, print one line with one integer: The number of occurrences of the most frequent value within the given range.

Sample Input

- -        

Sample Output

Source

Ulm Local 2007

（转自http://poj.org/problem?id=3368）

---

　　先讲一下题目大意，给出一个有n个数的不下降数列，和q个问题每个问题是求[a,b]中出现次数最多的数出现的次数，

有多组测试数据，当n = 0时测试结束

　　方法有多种，第一种直接暴力枚举，就不讲了

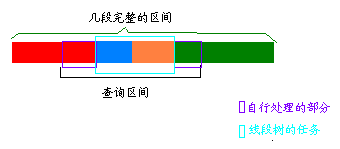
　　第二种用线段树，很多时候都不是完整的区间，怎么查？

　　左右两端不完整区间连续的个数是可以求出来的,这个就比较简单，记录一下每个区间开始的位置

，然后再弄个数组，记录第i个数属于的区间的新编号，如果a不是一个短的开始就就用下一个区间的

开始减去a （就把编号 + 1就是下一个区间的编号），结束部分就基本一样了

　　中间完整的区间就交给线段树查，最好是

　　把一个区间当成长度为1的线段，建树，查的时候就对应这个编号就行了。

由于我不想写，所以就不给代码了，可以在网上查查

　

　　第三种使用RMQ，反正又不会更新，再比较查询的时间复杂度，线段树的查询是O（log₂N），而ST算法的查询时间O（1）（自行忽略

log函数执行的时间或者打表的时间），线段树建树的时间复杂度貌似是O（2N）左右（大约实际有效的节点是原数组的2

倍），ST算法的预处理时间是O（nlog₂n)看起来差不多

　　ST算法的思路和上面差不多，两端单独处理，中间交给ST算法去查。

另外：

　　1.用位运算时一定要加上括号，位运算优先级很低，之前没在意，RE了几次

　　2.每次完成一轮计算该清0的清0，该还原的还原

Code

 #include<iostream>
 #include<cstdio>
 #include<vector>
 #include<cmath>
 using namespace std;
 typedef class MyData{
     private:
         MyData(int from,int end,int _count):from(from),end(end),_count(_count){}
     public:
         int from;
         int end;
         int _count;
         MyData(){}
         static MyData getNULL(){
             return MyData(,,);
         }
 }MyData;
 vector<MyData> list;
 int a = -,b;
 int *pos;
 int count1;
 int f[][];
 int t;
 int n,q;
 void init(){
     const int limit = list.size();
     for(int i = ;i < limit;i++)
         f[i][] = list[i]._count;
     for(int j = ; ( << j) < limit;j++){
         t =  << j;
         for(int i = ; i < limit && (i + t) < limit; i++){
             f[i][j] = max(f[i][j - ], f[ i + ( <<  j - ) ][j - ]);　　//位运算优先级低！！！打括号
         }
     }
 }
 int main(){
     while(true){
         scanf("%d",&n);
         if(n == ) break;
         scanf("%d",&q);
         pos = new int[(const int)(n + )];
         for(int i = ;i <= n;i++){
             scanf("%d",&b);
             if(a == b){
                 list[list.size() - ]._count++;
                 pos[i] = pos[i - ];
             }else{
                 if(!list.empty())
                     list[list.size() - ].end = i - ;
                 list.push_back(MyData::getNULL());
                 pos[i] = count1++;
                 list[list.size() - ].from = i;
                 list[list.size() - ]._count = ;
             }
             a = b;
         }
         list[list.size() - ].end = n;
         init();
         for(int i = ;i <= q;i++){
             scanf("%d%d",&a,&b);
             if(pos[a] == pos[b]){
                 printf("%d\n",b - a + );
                 continue;
             }
             if(pos[b] - pos[a] == ){
                 int result = max(list[pos[a]].end - a + ,b - list[pos[b]].from + );
                 printf("%d\n",result);
                 continue;
             }
             int ans = ;
             ans = max(list[pos[a]].end-a+,b-list[pos[b]].from+);
             b = pos[b] - ;
             a = pos[a] + ;
             int k = (int)(log((double)b-a+1.0)/log(2.0));
             int t2 = max(f[a][k],f[b-(<<k)+][k]);
             ans = max(ans,t2);
             printf("%d\n",ans);
         }
         delete[] pos;
         list.clear();
         count1 = ;
         a = -;
     }
     return ;
 }

---

[后记]

　　附赠调试这道题时所用的对拍器、比较程序和数据生成器

cmp.cpp:

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 char buf1[];
 char buf2[];
 FILE *fin1;
 FILE *fin2;
 int main(int argc, char* argv[]){
     fin1 = fopen(argv[],"r");
     fin2 = fopen(argv[],"r");
     while(!(feof(fin1))&&!(feof(fin2))){
         fscanf(fin1,"%s",buf1);
         fscanf(fin2,"%s",buf2);
         if(strcmp(buf1, buf2) != )    return ;
     }
     if(feof(fin1) != feof(fin2)) return ;
     return ;
 }

md_fv.cpp:

#include<iostream>
#include<fstream>
#include<cstdlib>
#include<time.h>
using namespace std;
ofstream fout("fv.in");
int main(){

    srand((unsigned)time(NULL));

    int n = rand()% + ;
    int q = rand()% + ;

    fout<<n<<" "<<q<<endl;

    int start = rand()% - ;
    for(int i =; i<= n;i++){
        start += rand()%;
        fout<<start<<" ";
    }

    fout<<endl;
    for(int i = ;i < q;i++){
        start = rand()%n + ;
        int end = min(rand()%(n - start + ) + start,n);
        fout<<start<<" "<<end<<endl;
    }

    fout<<""<<endl;
    return ;
}

test_fv.cpp:

 #include<iostream>
 #include<cstdlib>
 #include<time.h>
 using namespace std;
 typedef bool boolean;
 int statu;
 boolean aFlag;
 int main(){
     system("g++ fv.cpp -o fv.exe");
     system("g++ cmp.cpp -o cmp.exe");
     system("g++ md_fv.cpp -o md_fv.exe");
     system("g++ std.fv.cpp -o std.fv.exe");
     for(int i = ;i < ;i++){
         aFlag = true;
         system("md_fv");
         system("std.fv");
         clock_t begin = clock();
         statu = system("fv");
         clock_t end = clock();
         cout<<"测试数据#"<<i<<":";
         if(statu != ){
             cout<<"RuntimeError";
         }else if(system("cmp fv1.out fv.out") != ){
             cout<<"WrongAnswer";
         }else{
             cout<<"Accepted";
             aFlag = false;
         }
         cout<<"\t\tTime:"<<(end - begin)<<"ms"<<endl;
         if(aFlag){
             system("pause");
         }
     }
     return ;
 }