11.Container With Most Water---两指针

题目链接：https://leetcode.com/problems/container-with-most-water/description/

题目大意：给出一串数组(a1, a2, a3, ...an)，表示坐标(i, ai)，同样表示一条直线是从(i, 0)到(i, ai)，从中选出两条直线，计算其容器能蓄水多少，并找出最多的蓄水量。（容器不能倾斜，就是两条直线可以是不同高度，但是蓄水量要按照低高度的那条直线来计算），例子如下：

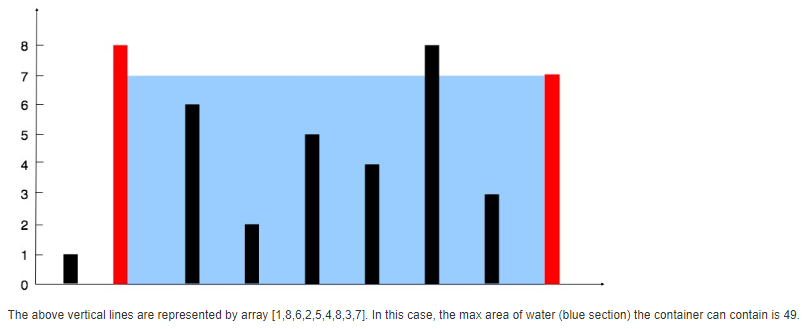
法一：暴力，对于一条直线，分别遍历左边和右边直线，计算其蓄水量，取最大者。可惜超时了。代码如下：

     public int maxArea(int[] height) {
         int res = 0;
         for(int i = 0; i < height.length; i++) {
             //计算左边直线
             for(int j = height.length - 1; j > i; j--) {
                 if(height[j] >= height[i]) {
                     res = Math.max(res, (j - i) * height[i]);
                     break;
                 }
             }
             //计算右边直线
             for(int j = 0; j < i; j++) {
                 if(height[j] >= height[i]) {
                     res = Math.max(res, (i - j) * height[i]);
                     break;
                 }
             }
         }
         return res;
     }

法二：两指针移动，与42题的两指针移动类似但略有区别，左指针与右指针相比较，记录较大者，若左指针较小，则从左往右移动，若右指针较小，则从右往左移动，如果当前值比较大者大，则计算：(较大者下标-当前值下标)*当前值高度，计算得到最后的结果。代码如下（耗时8ms）：

     public int maxArea(int[] height) {
         int res = 0, left = 0, right = height.length - 1;
         while(left < right) {
             //如果左指针<=右指针
             if(height[left] <= height[right]) {
                 while(left < right && height[left] <= height[right]) {
                     res = Math.max(res, (right - left) * height[left++]);
                 }
             }
             //如果左指针>右指针
             else {
                 while(left < right && height[left] > height[right]) {
                     res = Math.max(res, (right - left) * height[right--]);
                 }
             }
         }
         return res;
     }