LDA学习之beta分布和Dirichlet分布

---恢复内容开始---

今天学习LDA主题模型，看到Beta分布和Dirichlet分布一脸的茫然，这俩玩意怎么来的，再网上查阅了很多资料，当做读书笔记记下来：

先来几个名词：

共轭先验：

在贝叶斯统计理论中，如果某个随机变量Θ的后验概率 p(θ|x)和他的先验概率p(θ)属于同一个分布簇的，那么称p(θ|x)和p(θ)为共轭分布，同时，也称p(θ)为似然函数p(x|θ)的共轭先验。简言之，共轭就是我俩天生一对。我们后面会看到，多项分布的先验概率分布和其后验概率分布就是共轭的。

ok，下面我们来看看啥叫分布的分布：

还是抛硬币的实验，假设抛了5次硬币，出现了3次正面，你根据极大似然估计得出，抛一次硬币出现正面的概率是0.6。

但是这是绝对的吗？如果出现了2次正面呢？那得到的抛一次硬币出现正面的概率就是0.4了。

(下图是极大似然估计计算的过程)

然后你就会想到，哦，也许实际的概率是满足一定的分布的，我们实际实验的观测值得到的结果总是出自这个分布，一般都在最大值附近出现，比如0.5。

因此，人们引入了概率分布的先验概率：

比如说，在上述例子中，你觉得抛硬币出现正面的分布如下，他在0.8取得了最大值，也就是我们在抛硬币前认为这个硬币的若干组观测实验后计算的结果大部分在0.8附近。

好，假设你做了一组观测实验，我们可以通过上面定义的后验概率计算公式计算根据这组观测得到的后验概率，换言之，你调整了抛一次硬币出现正面的概率的分布，

或者说分布的分布。

好，下面问题来了，我怎么知道(假设)先验概率分布呢，这是个好问题，实际上可以任何种类的概率分布。你吐吐舌头，这和没说有啥区别。

别急，选择权在我们手中，既然可以选择任何种类的概率分布，我们干脆选一个性质好点的，容易计算的分布咯。

这个分布就是Beta分布：，其中，，x是[0 1]的随机变量。

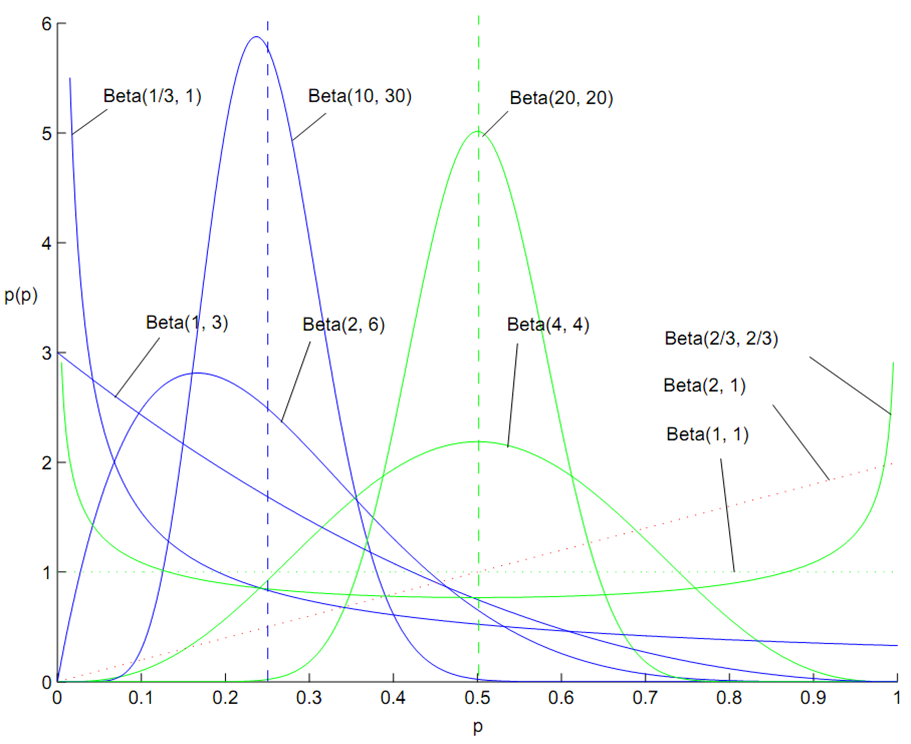
Beta分布不同参数下的结果如下图所示，可以看出，Beta分布形态各异，可以是凹的、凸的、单调上升的、单调下降的；可以是曲线也可以是直线，而均匀分布也是特殊的Beta分布。由于Beta 分布能够拟合如此之多的形状，因此它在统计数据拟合中被广泛使用。

好，还是上面抛硬币的例子，可以得到：(其中X是5次抛硬币试验中出现三次的观测事件)

下面计算P(X)：即X在先验概率下各种情况的条件概率和(或积分)

再计算后验概率就可以得到：

这里，2=5-3，也就是后验概率为，其中。

从上面的公式我们看到，抛一次硬币出现正面的概率的 先验概率分布和其对应的后验概率分布是共轭的，这就会选择Beta分布的好处所在。

还是上面的例子，新的后验概率为：

即，新的最大值在实际观测得到的似然函数值0.6和先验概率中的0.8之间，这是根据先验概率和观测结果共同得到的更具肯定性的结论。

上面讨论了二维的情况，也就是只有两个参数(抛硬币出现正面的概率和抛硬币出现反面的概率)，他们相加为1,如果有多个参数呢？(比如，掷一次骰子每个面出现的概率)。

这个时候使用同样的过程使用的就是Dirichlet Distribution。

假设有先验分布(比如，对应掷骰子的例子，k为6)：

观测实验得到的似然函数为：（多项分布计算公式）

那么可以计算得到后验概率分布为：

下面给出Dirichlet分布的概率密度函数为：

，其中

比如三维的Dirichlet Distribution如下：

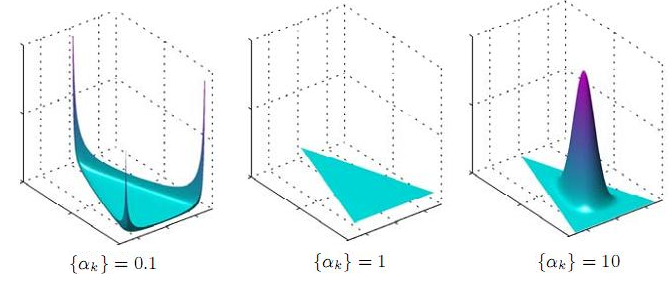
最后在概率论中，Dirichlet Distribution和Beta Distribution都叫做Conjugate Prior。根据不同的likelihood function，选择对应的conjugate prior作为对p(\theta)事先的估计(也就是先验概率分布)。

一个好的选择如下，可见二项分布使用的是Beta Distribution，多项分布使用的是Dirichlet Distribution。

可以看出，Beta分布是针对二项分布B(n，P)中参数P的分布的估计，其先验分布和后验分布是共轭的。而Dirichlet分布是针对多项分布中k各参数的估计，其先验分布和后验分布也是共轭的。这样，我们就可以用Beta分布去计算二项分布中的P，用Dirichlet分布去估计多项分布中的参数。

参考资料：

http://maider.blog.sohu.com/306392863.html

http://cos.name/2013/01/lda-math-beta-dirichlet/#more-6953

http://blog.163.com/zzz216@yeah/blog/static/162554684201381382117133/

etc...