Dirichlet Distribution
Beta分布:


二项式分布(Binomial distribution):

多项式分布:

Beta分布:

Beta分布是二项式分布的共轭先验(conjugate prior)

Dirichlet Distribution:


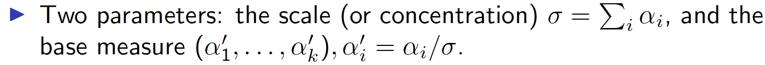


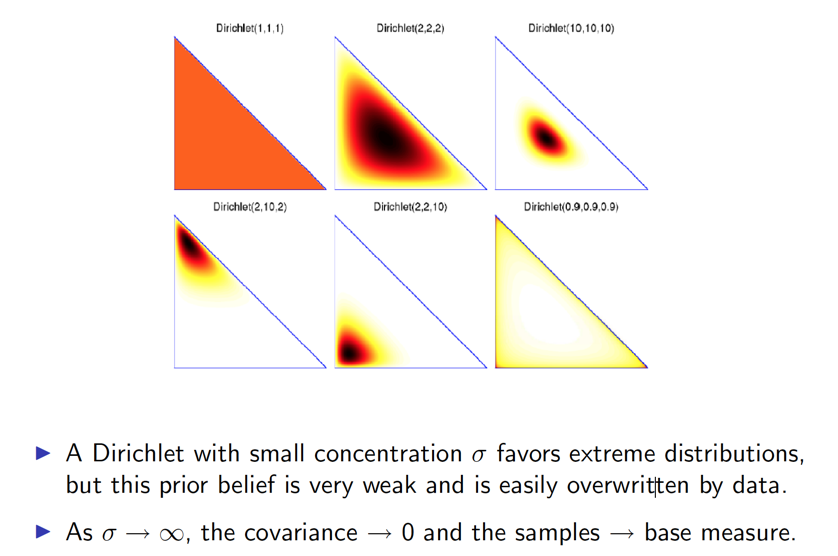



共轭先验可以使得先验分布和后验分布的形式相同
如果先验分布和似然函数可以使得先验分布和后验分布有相同的形式,那么就称先验分布与似然函数是共轭的
| likelihood 似然函数 | conjugate prior 共轭先验 | posterior 后验 |
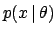 |
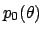 |
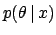 |
Normal 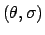 均匀分布 均匀分布 |
Normal 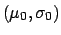 |
Normal 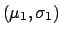 [Eqs. (30)-(32)] [Eqs. (30)-(32)] |
Binomial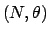 二项分布 二项分布 |
Beta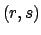 |
Beta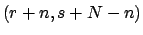 |
Poisson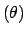 泊松分布 泊松分布 |
Gamma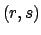 |
Gamma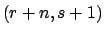 |
Multinomial 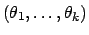 多项式分布 多项式分布 |
Dirichlet 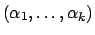 |
Dirichlet 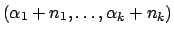 |
Dirichlet Distribution的更多相关文章
- The Dirichlet Distribution 狄利克雷分布 (PRML 2.2.1)
The Dirichlet Distribution 狄利克雷分布 (PRML 2.2.1) Dirichlet分布可以看做是分布之上的分布.如何理解这句话,我们可以先举个例子:假设我们有一个骰子,其 ...
- Notes on the Dirichlet Distribution and Dirichlet Process
Notes on the Dirichlet Distribution and Dirichlet Process In [3]: %matplotlib inline Note: I wrote ...
- [Bayes] Multinomials and Dirichlet distribution
From: https://www.cs.cmu.edu/~scohen/psnlp-lecture6.pdf 不错的PPT,图示很好. 伯努利分布 和 多项式分布 Binomial Distribu ...
- [综] Latent Dirichlet Allocation(LDA)主题模型算法
多项分布 http://szjc.math168.com/book/ebookdetail.aspx?cateid=1&§ionid=983 二项分布和多项分布 http:// ...
- Study notes for Latent Dirichlet Allocation
1. Topic Models Topic models are based upon the idea that documents are mixtures of topics, where a ...
- mahout系列----Dirichlet 分布
Dirichlet分布可以看做是分布之上的分布.如何理解这句话,我们可以先举个例子:假设我们有一个骰子,其有六面,分别为{1,2,3,4,5,6}.现在我们做了10000次投掷的实验,得到的实验结果是 ...
- 伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布与他们之间的关系,以及在LDA中的应用
在看LDA的时候,遇到的数学公式分布有些多,因此在这里总结一下思路. 一.伯努利试验.伯努利过程与伯努利分布 先说一下什么是伯努利试验: 维基百科伯努利试验中: 伯努利试验(Bernoulli tri ...
- LDA-Latent Dirichlet Allocation 学习笔记
以下内容主要基于<Latent Dirichlet Allocation>,JMLR-2003一文,另加入了一些自己的理解,刚开始了解,有不对的还请各位指正. LDA-Latent Dir ...
- LDA学习之beta分布和Dirichlet分布
---恢复内容开始--- 今天学习LDA主题模型,看到Beta分布和Dirichlet分布一脸的茫然,这俩玩意怎么来的,再网上查阅了很多资料,当做读书笔记记下来: 先来几个名词: 共轭先验: 在贝叶斯 ...
随机推荐
- 15个重要Python面试题 测测你适不适合做Python?
http://nooverfit.com/wp/15%E4%B8%AA%E9%87%8D%E8%A6%81python%E9%9D%A2%E8%AF%95%E9%A2%98-%E6%B5%8B%E6% ...
- Python Post and Get 登陆web后台系统并抓取页面
#coding=utf8 #! /usr/bin/env python import httplib import re import socket import urllib timeout = 6 ...
- TP框架M方法 create方法丢失字段问题
TP框架M方法 create方法丢失字段问题! thinkphp框架M方法 create方法丢失字段问题! thinkphp框架M方法 add方法字段丢失问题! 数据库 表新增了字段,用create方 ...
- Arrays.asList的用法
使用工具类Arrays.asList()把数组转换成集合时,不能使用其修改集合相关的方法,它的add/remove/clear方法会抛出UnsupportOperationException异常说明: ...
- 按钮CSS样式
CreateTime--2017年5月5日11:23:18Author:Marydon 按钮CSS样式 实现效果: <input type="button" onclic ...
- iOS 全屏侧滑/UIScrollView/UISlider间滑动冲突
代码地址如下:http://www.demodashi.com/demo/13848.html 效果预览 一.前期准备 有一个支持全屏侧滑返回的视图控制器ViewController,ViewCont ...
- nginx代理tomcat
http://blog.csdn.net/kongqz/article/details/6838989 http://www.800l.com/linux-nginx-tomcat-jdk.html ...
- Android系统示例分析之AccelerometerPlay
程序界面: 创建 SimulationView , 实现接口 SensorEventListener , 实现接口中两个抽象方法 public void onSensorChanged(SensorE ...
- 【RESTful风格】软件接口设计中RESTful风格
REST = Representational State Transfer 表述性状态转移,是一种软甲接口设计风格.总之就是一种风格 REST基于:HTTP.HTML.JSON.XML.URI 这些 ...
- OpenCV iOS开发(一)——安装(转)
OpenCV是一个开源跨平台的的计算机视觉和机器学习库,可以用来做图片视频的处理.图形识别.机器学习等应用.本文将介绍OpenCV iOS开发中的Hello World起步. 安装 OpenCV安装的 ...
