【学习记录】二分查找的C++实现，代码逐步优化

二分查找的思想很简单，它是针对于有序数组的，相当于数组（设为int a[N]）排成一颗二叉平衡树（左子节点<=父节点<=右子节点），然后从根节点（对应数组下标a[N/2]）开始判断，若值<=当前节点则到左子树，否则到右子树。查找时间复杂度是O(logN)，因为树的高度是logN。

二分查找分两种：一种是精确查找某个元素x，另一种则是根据比较关系式查找，比如返回i使得对任意j<i均有a[j]<a[i]，这用在折半插入排序中。

刚好前天无聊不借助STL手写折半插入排序时，发现自己基本功不扎实，对比了下STL自己实现的二分查找，发现自己还是太嫩了。

函数签名采用C风格的template <typename> T* f(T* a, size_t n, const T& x); 即查找区间为数组T a[n]整个区间，返回找到元素的地址。

下面给出对第一种查找的我第一感觉的实现方法

template <typename T>
T* binary_search(T* a, size_t n, const T& x)
{
    size_t low = ;
    size_t high = n - ;
    size_t mid = (low + high) / ;
    while (low < mid)
    {
        if (x == a[mid])
            return a + mid;
        else if (x < a[mid])  // x位于[low, mid)区间
            high = mid - ;   // 缩小查找范围到[low, mid-1]
        else // x > a[mid]
            low = mid + ;    // 缩小查找范围到[mid+1, high]
        mid = (low + high) / ;
    }
    return nullptr;  // 查找失败
}

测试代码如下

#include "binary_search.h"
#include <cstdio>

int main()
{
    const size_t N = ;
    int a[N] = {,,,,,,,};
    auto p = binary_search(a, N, );
    if (p != nullptr)
        printf("a[%d] = %d\n", p - a, *p);
    return ;
}

结果什么也没输出。调试发现在mid=2时由于low=2此时while循环退出，而此时本应该比较一下x和a[mid]的。

肉眼调试，初始：low=0, high=7, mid=(0+7)/2=3，进入while循环。

low=0<3=mid，a[3]=4>3，设置high=3，计算mid=(0+3)/2=1，进入下次循环

low=0<1=mid，a[1]=2<3，设置low=2，计算mid=(2+3)/2=2，进入下次循环

low=2=mid，跳出循环。返回默认返回值nullptr

可能这里会想说，那把while的条件改成<=不就行了？这样会造成死循环，因为(a+b)/2>=a恒成立。

那么让相等的时候比较一次就退出呢？

也不行，假如low=0，high=1，mid永远等于0，最可怕的是，这时候不会跟a[1]进行比较。

正是第一感觉考虑到这个，所以我没有用while (low < high)，因为此时也会死循环。

——根本问题出现了，二分法每次都会对半切分区间，但是有时候区间大小（减1）为奇数，那么两个子区间大小肯定不一样。

对两个数组下标low和high（low<=high），按照(low+high)/2得到的mid把数组划分成哪两部分呢？

对于所有对半缩小区间问题，最后都会变成2种情况：1、low=mid=high；2、low=mid=high-1。

设k为整数：

假如low+high=2k，那么mid=k，左区间[low, mid-1]大小为mid-low=k-low，右区间[mid+1,high]大小为high-k=2k-low-k=k-low，左右区间相等；

假如low+high=2k+1，那么mid=k，左区间大小仍为k-low，右区间大小为2k+1-low-k=k-low+1，比左区间多1个。

也就是如果仍然以while (low<high)来判断，那么在结束循环后，在return nullptr;之前要加下面几行代码判断。

    if (a[mid] == x)  // low == mid
        return a + mid;
    if (low < high && a[high] == x)  // low == mid == high-1
        return a + high;

稍微显得不太美观了，能不能一个while循环就搞定还不用做额外判断的呢？

考虑下STL采用的的左闭右开区间[first, last)，对数组a[N]而言first=0，last=N，不用特地写N-1。

假如first+last=2k，那么mid=k，左区间[first, mid)大小为mid-first=k-first，右区间[mid+1, last)大小为(2k-first)-(mid+1)=k-first-1，比左区间少1个。

假如first+last=2k+1，两个区间一样大（这里不给出计算流程了）。 给出这种情况下的代码

T* binary_search(T* a, size_t n, const T& x)
{
    size_t first = ;
    size_t last = n;
    size_t mid = (first + last) / ;
    while (first < mid)
    {
        if (x == a[mid])
            return a + mid;
        else if (x < a[mid])
            last = mid;  // [first, mid)
        else // x > a[mid], [mid+1, last)
            first = mid + ;
        mid = (first + last) / ;
    }
    if (a[mid] == x)
        return a + mid;
    return nullptr;
}

测试代码

    for (int x = ; x <= ; x++)
    {
        auto p = binary_search(a, N, x);
        if (p != nullptr)
            printf("a[%d] = %d\n", p - a, *p);
    }

结果无误，突然觉得STL采用左闭右开区间有其道理了。虽然感觉代码还是有些丑陋，再删一行的话充其量就是写成while ((mid = (first + last) / 2) > first)的形式，减少了while循环体内的一行重复代码mid = (first + last) / 2;

这样就完了？NO！这种实现健壮性不够，因为会出现溢出！

从最开始我就错了！假设，这里仅仅是假设，size_t的上限为3，即2 bits 无符号整数。当first为1（01），last为3（11）时，两者相加会溢出（超出size_t能表示的范围[0, 4)）

理想的结果本来是2，实际结果（假如运算规则是超出最高位的进位直接省略掉）

二进制运算01 + 11 = 100，省略最高位1，变成了00，然后00除以2，结果是00，即0。也就是(1+3)/2的结果不是2，而是0！

当然，像我这种比较随意的简单测试不会出现溢出情况，但是溢出的风险必须考虑！（想起当时刷了道二分法的leetcode题应该就是挂在这里了）

因此：mid = (first + last) / 2要改成mid = first + (last - first) / 2

本着学习的态度，去看了官网上的binary_search的实现http://www.cplusplus.com/reference/algorithm/binary_search/

template <class ForwardIterator, class T>
  bool binary_search (ForwardIterator first, ForwardIterator last, const T& val)
{
  first = std::lower_bound(first,last,val);
  return (first!=last && !(val<*first));
}

调用了lower_bound函数，然后去看下lower_bound。先不看代码，这里我顺便去看了<algorithm>中除了lower_bound还有upper_bound，很直白的意思，下界和上界，按照STL的设计应该也是左闭右开，用测试代码描述如下：

#include <cstdio>
#include <algorithm>

int main()
{
    const size_t N = ;
    int a[N] = { ,,,, };
    auto itL = std::lower_bound(a, a + N, );
    auto itR = std::upper_bound(a, a + N, );
    printf("itL == a[%d]\n", itL - a);  // itL == a[1]
    printf("itR == a[%d]\n", itR - a);  // itR == a[5]
    return ;
}

注释部分为该行输出结果，lower_bound返回第1个与查找值相等的迭代器，upper_bound返回lower_bound开始第1个与查找值不等的迭代器。

这么说不太严密，因为数组中可能不存在与查找值相等的值。那么此时会返回什么？

测试代码如下

    const size_t N = ;
    double a[N] = { ,,,, };
    auto itL = std::lower_bound(a, a + N, );
    auto itR = std::upper_bound(a, a + N, );
    printf("itL == a[%d]\n", itL - a);  // itL == a[0]
    printf("itR == a[%d]\n", itR - a);  // itR == a[0]
    itL = std::lower_bound(a, a + N, 1.5);
    itR = std::upper_bound(a, a + N, 1.5);
    printf("itL == a[%d]\n", itL - a);  // itL == a[1]
    printf("itR == a[%d]\n", itR - a);  // itR == a[1]

严密又简洁点讲，在lower_bound左边的值都<查找值，在upper_bound左边的值都<=查找值。也就是我在开始提到的二分查找的第二种情况。

好了，那么回顾binary_search的代码，它调用的是lower_bound，第一行返回第1个与查找值相等的迭代器并赋值给first，若不存在则first为第1个大于查找值的迭代器。

第二行返回(first!=last && !(val<*first))，显然两个bool表达式同时成立等价于数组中含有查找值。

lower_bound什么时候表示能找到值？——当然是返回的迭代器对应值等于查找值，因为查找失败时，返回的是比该值大的迭代器，如果是我的话会直接写一句return val==*first。——但是不对，因为如果整个区间[first, last)的值都比查找值小，那么返回的是last，一个无法访问的迭代器，对*first的比较就会出错。所以前面加了一句first != last。那么后面为什么用!(val<*first)（等价于*first<=val）来判断呢？

问题等价于——什么时候查找成功并且*first<val？

关于这点，我仔细思考了一下，不知回答是否正确。

首先，这种情况是不存在的；

其次，这么写是因为这是函数模板，可能进行比较的是类（而非基本数据类型），而这里只要求类重载了operator<用来比较，对于operator==甚至operator>都可有可无

OK，现在来看看lower_bound的实际实现

template <class ForwardIterator, class T>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last, const T& val)
{
  ForwardIterator it;
  iterator_traits<ForwardIterator>::difference_type count, step;
  count = distance(first,last);
  while (count>)
  {
    it = first; step=count/; advance (it,step);
    if (*it<val) {                 // or: if (comp(*it,val)), for version (2)
      first=++it;
      count-=step+;
    }
    else count=step;
  }
  return first;
}

翻译成我之前的函数签名即如下代码（主要用于表达意思，没考虑细枝末叶的优化）

template <typename T>
T* binary_search(T* a, size_t n, const T& x)
{
    T* first = a;         // 搜索区间起始位置(左闭)
    T* last = a + n;      // 搜索区间结束位置(右开)
    ptrdiff_t count = n;  // 搜索区间元素数量
    while (count > )
    {
        ptrdiff_t step = count / ;
        T* mid = first + step;  // 二分点
        if (*mid < x) {  // 继续查找[mid+1, last)
            first = mid + ;
            count -= step + ;
        }
        else
            count = step;   // 继续查找[first, mid)
    }
    return first;
}

这里的关键点是while循环里的变成了区间数量count，而count不能简单地用last-first来代替，即使它的初始值为last-first！

依旧考虑特殊情况：对数组a[2]，first=0，last=2，count=2-0=2，进入while循环

count=2>0，计算step=2/2=1；mid=first+1，*mid即a[1]；

若a[1]<x则需要查找[2,2)，此时first变为mid+1=first+2，count变为2-(1+1)=0，last-first等于count；

否则，需要查找[0,1)，此时count变为1，但是last-first=2不等于count！

说白了是把用first和last表示区间[first, last)改成用first和count表示区间[first, first+count)

这么一想，用first和last一样能写出这样的代码啊！于是我尝试着改了下

template <typename T>
T* binary_search(T* a, size_t n, const T& x)
{
    T* first = a;         // 搜索区间起始位置(左闭)
    T* last = a + n;      // 搜索区间结束位置(右开)
    while (last - first > )
    {
        ptrdiff_t step = (last - first) / ;
        if (first[step] < x)   // first + step为二分点mid
            first += (step + );  // 继续查找[mid+1, last)
        else
            last = first + step;  // 继续查找[first, mid)
    }
    return first;
}

这样的代码看起来思路更加自然，而且没有什么漏洞（不考虑对类型T的要求的话）

再反思之前的做法，用起始位置和mid比较是不合适的，迭代的终止条件应该是搜索子区间元素数量大于0！

我的实现思路从第一步就错了！也没必要去计算左区间大还是右区间大！因为终止条件是“当前区间”不为空！而不需要比较二分点和下界或者上界。

最后给出最终的二分搜索代码（使用first和last表示左闭右开区间）

/**
* 功能: 在升序排好的数组a[n]用二分法查找元素x的位置
* 参数:
*   @a 数组首地址
*   @n 数组元素数量
*   @x 要查找的元素
* 返回: 若a[n]中存在元素x，返回任意一个与x相等的数组元素地址; 否则返回nullptr.
*/
template <typename T>
T* binary_search(T* a, size_t n, const T& x)
{
    size_t first = ;
    size_t last = n;
    while (last - first > )
    {
        size_t mid = first + (last - first) / ;
        if (a[mid] == x)
            return a + mid;
        else if (a[mid] < x)
            first = mid + ;
        else
            last = mid;
    }
    return nullptr;
}

用闭区间low和high就稍微复杂点，因为high可能为-1，如果不把high的类型改为int，while里面需要额外判断high!=-1，即while (high - low >= 0 && high != -1)

测试代码和测试结果如下

#include "binary_search.h"
#include <cstdio>

int main()
{
    const size_t N = ;
    int a[N] = { ,,,,,,, };
    for (size_t i = ; i < N; i++)
        a[i] = i + ;
    for (int x = ; x <= ; x++)
    {
        auto p = binary_search(a, N, x);
        if (p != nullptr)
            printf("a[%d] = %d\n", p - a, *p);
        else
            printf("%d not found!\n", x);
    }
    return ;
}

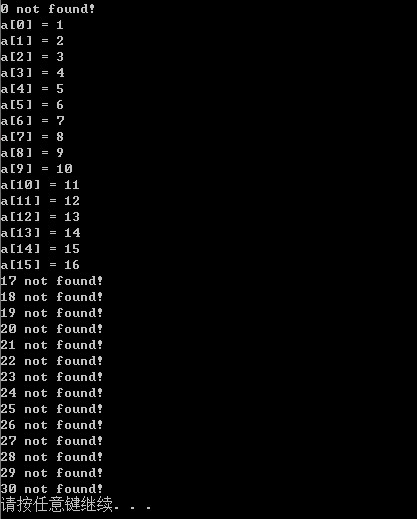
这篇博客虽然很啰嗦，而且基本功稍微扎实的都能看出我讲了一堆废话，但是主要目的还是记录我从错误的思路转向正确的过程，顺便温故了STL关于二分查找的函数。