NB二人组（二）----归并排序

归并排序的思路：

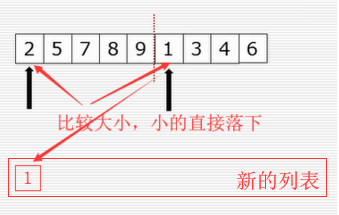
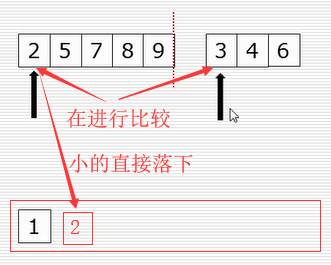
归并算法程序（配合下图进行思考）：

def merge(li,low,mid,high):
    i = low
    j = mid + 1
    ltmp=[]
    while i <= mid and j <= high: # 左边有数 且 右边也有数
        if li[i] < li[j]: # 左边小于右边
            ltmp.append(li[i]) # 把左边的数 添加到 ltmp 这个列表中
            i += 1 # 右移一位
        else:
            ltmp.append(li[j]) # 右边小于左边
            j += 1 # 右移
    while i <= mid: # 如果左边有剩余
        ltmp.append(li[i]) # 将剩余的加入ltmp列表
        i += 1 # 右移
    while j <= high: # 如果右边有剩余
        ltmp.append(li[j]) # 将剩余的加入ltmp列表
        j += 1 # 右移
    li[low:high+1] = ltmp # 将ltmp这个列表里的数 传给 li 这个列表

li = [1,4,6,7,9,2,3,5,8]
merge(li,0,4,8)
print(li)

打印出来的效果图为：

有了归并怎么用？

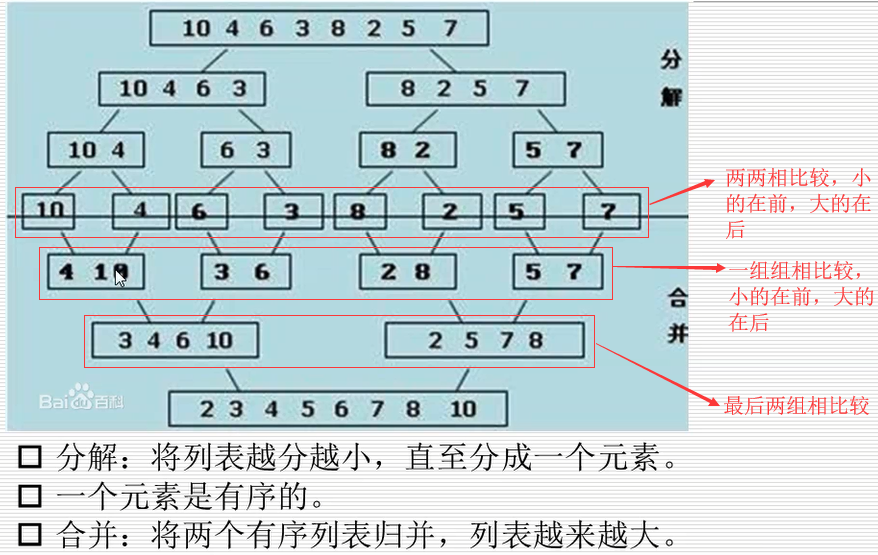
def merge(li,low,mid,high):
    i = low
    j = mid + 1
    ltmp=[]
    while i <= mid and j <= high: # 左边有数 且 右边也有数
        if li[i] < li[j]: # 左边小于右边
            ltmp.append(li[i]) # 把左边的数 添加到 ltmp 这个列表中
            i += 1 # 右移一位
        else:
            ltmp.append(li[j]) # 右边小于左边
            j += 1 # 右移
    while i <= mid: # 如果左边有剩余
        ltmp.append(li[i]) # 将剩余的加入ltmp列表
        i += 1 # 右移
    while j <= high: # 如果右边有剩余
        ltmp.append(li[j]) # 将剩余的加入ltmp列表
        j += 1 # 右移
    li[low:high+1] = ltmp # 将ltmp这个列表里的数 传给 li 这个列表

def mergesort(li,low,high):
    if low < high:
        mid = (low + high) // 2
        mergesort(li,low,mid)   # 先分解
        mergesort(li,mid+1,high)   # 先分解
        merge(li,low,mid,high)   # 在合并

li = [1,4,6,7,9,2,3,5,8,]
mergesort(li,0,8)
print(li)