「ZJOI2017」仙人掌

「ZJOI2017」仙人掌

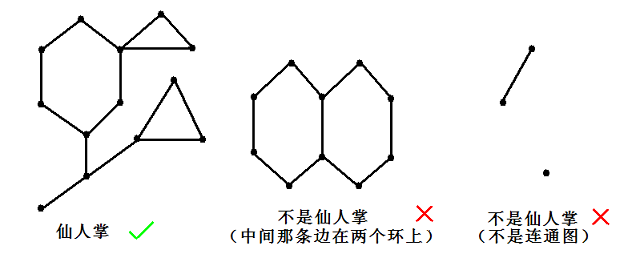
题目大意：

给定一张无向联通图，求有多少种本质不同的不加重边的加边方案使得新图是个仙人掌。

解题思路：

如果原来的图不是仙人掌，那么答案就是 \(0\) ，否则求出这个仙人掌的无向图 \(\text{dfs}\) 树，任何一条新边都不能覆盖原来已经被覆盖过的边。那么只要把已经覆盖过得边删掉，变成若干棵树的问题，答案就是每棵树的答案的乘积。

一棵树的做法有一个很厉害的转化，因为题目要求不能有重边，我们可以允许转移加重边，并且每条树边必须被覆盖。然后会发现把每一种这样的方案删去重边后，新图就是一个合法图，且和要求的方案一一对应。

那么问题就转化为除了根以外，每一棵子树都要向子树外连恰好一条边的方案数。

考虑节点 \(u\) 是根节点，那么 \(dp(u)=w(size)\prod dp(v)\) ，\(w(size)\) 为 \(size\) 个点互相连边，每个点度数 \(\leq 1\) 的方案数，\(size\) 是 \(u\) 的儿子数量。可以理解为，每个儿子的子树要么连到别的儿子的子树里，要么连到 \(u\) 。

考虑怎么求 \(w(n)\) ，直接考虑组合意义，第 \(n\) 个点要么不连边，要么在前面选另外一个点和它连边。

\[w(n)=w(n-1)+w(n-2)\times (n-1)
\]

考虑节点 \(u\) 不是根节点的情况，要选出一个点和子树外连边，分两种情况讨论。

1. 选出的点是 \(u\) ，方案数就是 \(w(size)\)
2. 选出的点是子树内的某个点，那么就选一个子树向外连，其它还是正常连，方案数是 \(w(size-1)\times size\)

那么总方案数就是 \(w(size)+w(size-1)\times size =w(size+1)\) 。

然后就做完了，复杂度 \(\mathcal O(n)\) 。

code

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
    int ch = 0, f = 0; x = 0;
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
    for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
    if(f) x = -x;
}
const int N = 500005, mod = 998244353;
map<int, int> ban[N];
vector<int> g[N];
int dfn[N], sum[N], dp[N], w[N], isr[N], n, m, Index;
inline void dfs1(int u, int fa){
	dfn[u] = ++Index;
	for(int i = 0; i < (int) g[u].size(); i++){
		int v = g[u][i];
		if(v == fa) continue;
		if(dfn[v]){
			ban[u][v] = 1;
			if(dfn[v] < dfn[u]) sum[u]++, sum[v]--;
		}
		else dfs1(v, u);
	}
}
inline int dfs2(int u){
	for(int i = 0; i < (int) g[u].size(); i++)
		if(dfn[g[u][i]] > dfn[u] && !ban[u][g[u][i]]){
			if(dfs2(g[u][i])) return 1;
			sum[u] += sum[g[u][i]];
		}
	if(sum[u] > 1) return 1;
	if(sum[u] == 1) isr[u] = 1; return 0;
}
inline void dfs3(int u){
	int size = 0; dp[u] = 1;
	for(int i = 0; i < (int) g[u].size(); i++){
		int v = g[u][i];
		if(isr[v] || dfn[v] < dfn[u]) continue;
		size++;
		dfs3(v), dp[u] = 1ll * dp[u] * dp[v] % mod;
	}
	if(!size) return;
	if(isr[u]) dp[u] = 1ll * dp[u] * w[size] % mod;
	else dp[u] = 1ll * dp[u] * w[size+1] % mod;
}
int main(){
	w[0] = w[1] = 1;
	for(int i = 2; i < N; i++)
		w[i] = (1ll * w[i-2] * (i - 1) + w[i-1]) % mod;
	int T; read(T);
	while(T--){
		Index = 0;
		for(int i = 1; i <= n; i++)
			g[i].clear(), ban[i].clear(), dp[i] = dfn[i] = isr[i] = sum[i] = 0;
		read(n), read(m);
		for(int i = 1, x, y; i <= m; i++){
			read(x), read(y);
			g[x].push_back(y), g[y].push_back(x);
		}
		dfs1(1, 0);
		if(dfs2(1)){ puts("0"); continue; }
		int res = 1;
		isr[1] = 1;
		for(int i = 1; i <= n; i++) if(isr[i]){
			dfs3(i), res = 1ll * res * dp[i] % mod;
		}
		printf("%d\n", res);
	}
	return 0;
}