到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法
是更好的解决方案。如：

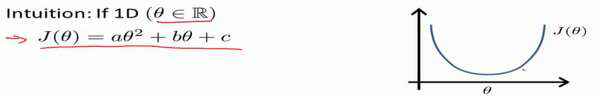
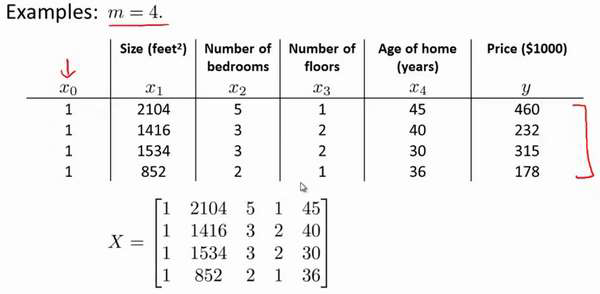
即：

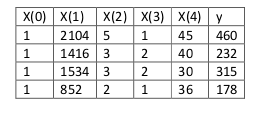
运用正规方程方法求解参数：

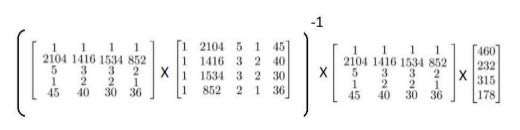
注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺
寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是
不能用的。

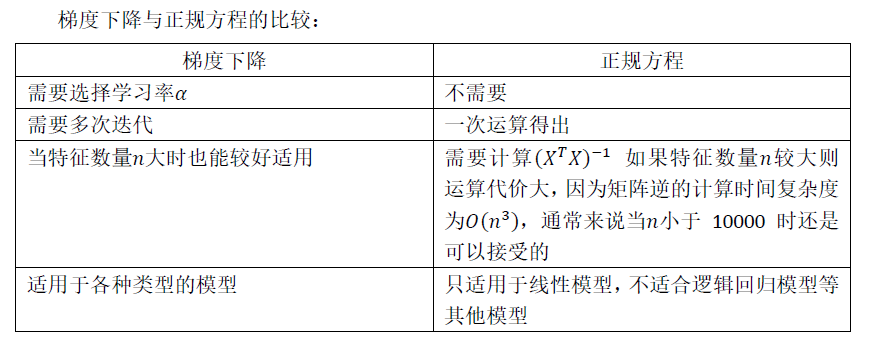
　　总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数

吴恩达机器学习笔记13-正规方程(Normal Equation)的更多相关文章

  1. [吴恩达机器学习笔记]13聚类K-means

    13.聚类 觉得有用的话,欢迎一起讨论相互学习~Follow Me 13.1无监督学习简介 从监督学习到无监督学习 在一个典型的监督学习中,我们有一个有标签的训练集,我们的目标是找到能够区分正样本和负 ...

  2. Coursera-AndrewNg(吴恩达)机器学习笔记——第二周

    一.多变量线性回归问题(linear regression with multiple variables) 搭建环境OctaveWindows的安装包可由此链接获取:https://ftp.gnu. ...

  3. 吴恩达机器学习笔记（六） —— 支持向量机SVM

    主要内容: 一.损失函数 二.决策边界 三.Kernel 四.使用SVM (有关SVM数学解释:机器学习笔记(八)震惊!支持向量机(SVM)居然是这种机) 一.损失函数 二.决策边界 对于: 当C非常 ...

  4. Machine Learning|Andrew Ng|Coursera 吴恩达机器学习笔记

    Week1: Machine Learning: A computer program is said to learn from experience E with respect to some ...

  5. Machine Learning|Andrew Ng|Coursera 吴恩达机器学习笔记(完结)

    Week 1: Machine Learning: A computer program is said to learn from experience E with respect to some ...

  6. 吴恩达机器学习笔记——正规方程（Normal Equation）

    问题描述:m examples : (x(1),y(1)), (x(2),y(2)),..., (x(m),y(m)) and n features; 计算方法:θ = (XTX)-1XTy; 计算过 ...

  7. Coursera-AndrewNg(吴恩达)机器学习笔记——第三周

    一.逻辑回归问题(分类问题) 生活中存在着许多分类问题,如判断邮件是否为垃圾邮件:判断肿瘤是恶性还是良性等.机器学习中逻辑回归便是解决分类问题的一种方法.二分类:通常表示为yϵ{0,1},0:&quo ...

  8. Machine Learning——吴恩达机器学习笔记（酷

    [1] ML Introduction a. supervised learning & unsupervised learning 监督学习:从给定的训练数据集中学习出一个函数(模型参数), ...

  9. [吴恩达机器学习笔记]12支持向量机5SVM参数细节

    12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.5 SVM参数细节 标记点选取 标记点(landma ...

随机推荐

  1. 处理ajax数据；数据渲染

    当我们用ajax把数据拿到前台,该如何渲染到页面,有以下几种方式: 一:使用字符串拼接的方法 声明一个空变量,然后拼接 var st=""; st+="<div&g ...

  2. MongoDB、PyMongo数据操作

    MongoDB 命令 C:\Program Files\MongoDB\Server\4.0\bin mongo 客户端 mongod 服务端 mongoexport 导出 普通格式,每条记录一行,整 ...

  3. 使用串口安装centos操作系统

    https://linuxconfig.org/how-to-force-text-mode-installation-of-redhat-linux https://www.centos.org/f ...

  4. Learning to Promote Saliency Detectors

    Learning to Promote Saliency Detectors 原本放在了思否上, 但是公式支持不好, csdn广告太多, 在博客园/掘金上发一下 https://github.com/ ...

  5. P2880 [USACO07JAN]平衡的阵容Balanced Lineup（RMQ的倍增模板）

    题面:P2880 [USACO07JAN]平衡的阵容Balanced Lineup RMQ问题:给定一个长度为N的区间,M个询问,每次询问Li到Ri这段区间元素的最大值/最小值. RMQ的高级写法一般 ...

  6. IIS配置支持跨域请求

    对于初次在IIS部署网站的同学,很容易忽略或不知道如何配置使其网站支持跨域请求,这里介绍一个最基础的方式,配置HTTP响应标头. 在IIS上选择HTTP响应标头,选择添加自定义响应标头,通常我们会添加 ...

  7. C#事务提交

    using (System.Transactions.TransactionScope transcope = new System.Transactions.TransactionScope()) ...

  8. HTML5-桌面提醒功能

    window.webkitNotifications.requestPermission(); statue = window.webkitNotifications.checkPermission( ...

  9. 在centos7上配置jenkins

    在Linux(centos7)环境下配置jenkins,并用github作为仓库. 配置jenkins https://blog.csdn.net/wangfei0904306/article/det ...

  10. P1081 开车旅行(Not Finish)

    https://www.luogu.org/problemnew/show/P1081