如果一对兔子每月生一对兔子；一对新生兔，从第二个月起就开始生兔子；假定每对兔子都是一雌一雄，试问一对兔子，第n个月能繁殖成多少对兔子？

———————————————————————————————————————————————————————————————————

典型斐波那契数列，用递归实现是so easy,在JS中实现递归通常用arguments.callee

这是因为早期JS没有具名函数，无法使用函数名进行递归，于是产生了arguments.callee

JS严格模式禁用了arguments.callee，这意味着无法在匿名函数中调用自身。

为什么要禁用呢？因为普通写法性能上比arguments更优，而且arguments.callee 还会带来函数引用优化问题和尾递归优化的问题

————————————————————————————————————————————————————————————————————

上述兔子问题，用递归的话，不到100次递归成功搞垮了我的浏览器，函数调用的次数呈指数级增长，性能堪忧，所以，，，，下面是斐波那契的非递归实现：

用迭代消除递归：

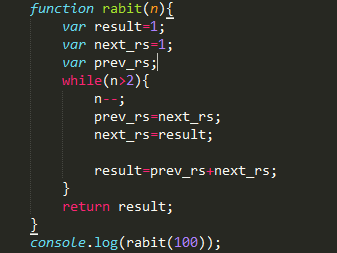
性能提升了几百万倍甚至更多

callee和斐波那契数列的更多相关文章

  1. C#求斐波那契数列第30项的值（递归和非递归）

    using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...

  2. 斐波拉契数列加强版——时间复杂度O(1)，空间复杂度O(1)

    对于斐波拉契经典问题,我们都非常熟悉,通过递推公式F(n) = F(n - ) + F(n - ),我们可以在线性时间内求出第n项F(n),现在考虑斐波拉契的加强版,我们要求的项数n的范围为int范围 ...

  3. js中的斐波那契数列法

    //斐波那契数列:1,2,3,5,8,13…… //从第3个起的第n个等于前两个之和 //解法1: var n1 = 1,n2 = 2; for(var i=3;i<101;i++){ var ...

  4. 剑指Offer面试题：8.斐波那契数列

    一.题目:斐波那契数列 题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项.斐波那契数列的定义如下: 二.效率很低的解法 很多C/C++/C#/Java语言教科书在讲述递归函数的时 ...

  5. 算法: 斐波那契数列C/C++实现

    斐波那契数列: 1,1,2,3,5,8,13,21,34,....     //求斐波那契数列第n项的值 //1,1,2,3,5,8,13,21,34... //1.递归: //缺点:当n过大时,递归 ...

  6. 洛谷P1962 斐波那契数列 || P1349 广义斐波那契数列[矩阵乘法]

    P1962 斐波那契数列 大家都知道,斐波那契数列是满足如下性质的一个数列: • f(1) = 1 • f(2) = 1 • f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数 ...

  7. Python递归及斐波那契数列

    递归函数 在函数内部,可以调用其他函数.如果一个函数在内部调用自身本身,这个函数就是递归函数.举个例子,我们来计算阶乘 n! = 1 * 2 * 3 * ... * n,用函数 fact(n)表示,可 ...

  8. 简单Java算法程序实现！斐波那契数列函数~

    java编程基础--斐波那契数列 问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 思路:可能出现的情况:(1) n=1 ,一种方法 ;(2)n=2 ...

  9. js 斐波那契数列（兔子问题）

    对于JS初学者来说,斐波那契数列一直是个头疼的问题,总是理不清思路. 希望看完这篇文章之后会对你有帮助. 什么是斐波那契数列 : 答: 斐波那契数列,又称黄金分割数列.因数学家列昂纳多·斐波那契(Le ...

随机推荐

  1. EmpireCMS的使用

    1.下载安装empirecms 下载完成后解压将upload目录整体上传到服务器,并更名为empirecms_test 更改目录文件的权限: chmod -R 777 empirecms_test 配 ...

  2. sql left join多表

    表A---------------------------------关联第一张表B-----------------------关联第二张表c select * fomr 表名A left join ...

  3. Nginx 优化缓冲区与传输效率

    L:126 这里简单的做个计算 比如 我的服务器带宽是 5M=41943040字节 如果按照公网用PIND的得到延迟结果 icmp_seq=3 ttl=49 time=35.612 ms BDP =  ...

  4. [BZOJ 2705] [SDOI 2012] Longge的问题

    Description Longge的数学成绩非常好,并且他非常乐于挑战高难度的数学问题.现在问题来了:给定一个整数 \(N\),你需要求出 \(\sum gcd(i, N)(1\le i \le N ...

  5. BZOJ1449[JSOI2009]球队收益&BZOJ2895球队预算——最小费用最大流

    题目描述 输入 输出 一个整数表示联盟里所有球队收益之和的最小值. 样例输入 3 3 1 0 2 1 1 1 10 1 0 1 3 3 1 2 2 3 3 1 样例输出 43 提示   要求总费用最低 ...

  6. Codeforces Round #449 Div. 1

    B:注意到nc/2<=m,于是以c/2为界决定数放在左边还是右边,保证序列满足性质的前提下替换掉一个数使得其更靠近边界即可. #include<iostream> #include& ...

  7. [USACO12MAR] 花盆Flowerpot

    类型:二分+单调队列 传送门:>Here< 题意:给出$N$个点的坐标,要求根据$x$轴选定一段区间$[L,R]$,使得其中的点的最大与最小的$y$值之差$\geq D$.求$Min\{R ...

  8. ☆ [POJ2559] Largest Rectangle in a Histogram 「单调栈」

    类型:单调栈 传送门:>Here< 题意:给出若干宽度相同的矩形的高度(条形统计图),求最大子矩形面积 解题思路 单调栈的经典题 显然,最终的子矩形高度一定和某一个矩形相等(反证).因此一 ...

  9. WEB请求处理

    https://blog.csdn.net/bpingchang/article/details/51328941

  10. Yahoo Programming Contest 2019 补题记录（DEF）

    D - Ears 题目链接:D - Ears 大意:你在一个\(0-L\)的数轴上行走,从整数格出发,在整数格结束,可以在整数格转弯.每当你经过坐标为\(i-0.5\)的位置时(\(i\)是整数),在 ...