agc032

T1 题意：你要进行n次操作，第i次选择一个数k∈[1,i]，并插入到当前序列的第k个位置。给定目标序列，输出操作序列。100,2s。

解：冷静分析一波，我们可以从后往前确定操作序列。这样每次确定一个操作之后就会删除一个数。

如果有a_i = i的位置那我们显然可以把这个i操作放到操作序列最后。如果有多个这样的i，从后往前处理。

 #include <bits/stdc++.h>

 const int N = ;

 int a[N], b[N];

 int main() {

     int n;
     scanf("%d", &n);
     for(int i = ; i <= n; i++) {
         scanf("%d", &b[i]);
     }
     for(int i = n; i >= ; i--) {
         bool f = ;
         for(int j = i; j >= ; j--) {
             if(b[j] > j) break;
             if(b[j] == j) {
                 a[i] = j;
                 //printf("a %d = %d \n", i, j);
                 for(int k = j; k < i; k++) {
                     b[k] = b[k + ];
                 }
                 f = ;
                 break;
             }
         }
         if(!f) {
             printf("-1");
             return ;
         }
     }
     for(int i = ; i <= n; i++) {
         printf("%d\n", a[i]);
     }
     return ;
 }

AC代码

T2 题意：构建一个n个点的简单无向连通图，使得每个点的邻居的编号之和相等。100,2s。

解：先玩一下3和4的时候，发现是一张完全二分图，且左右部的节点编号之和相等。

这启发我们把这些点分成k份，每份的编号之和相同。然后每个点向其他所有不是同类的点连边。

n为偶数的时候就是首尾配对，和为n + 1，n为奇数的时候提出n来然后首尾配对，和为n。

 #include <bits/stdc++.h>

 const int N = ;

 int vis[N];

 int main() {

     int n, cnt1 = ;
     scanf("%d", &n);
     int t = (n + ) * n / ;
     if(t & ) {
         if((n & ) == ) {
             printf("%d\n", n * (n - ) / );
             for(int i = ; i <= n; i++) {
                 for(int j = i + ; j <= n; j++) {
                     if(i + j != n + ) {
                         printf("%d %d \n", i, j);
                     }
                 }
             }
             return ;
         }
         else {
             printf("%d \n", (n - ) * (n - ) /  + n - );
             for(int i = ; i < n; i++) {
                 printf("%d %d \n", i, n);
             }
             for(int i = ; i < n; i++) {
                 for(int j = i + ; j < n; j++) {
                     if(i + j != n) {
                         printf("%d %d \n", i, j);
                     }
                 }
             }
         }
         return ;
     }
     t /= ;
     for(int i = n; i >=  && t; i--) {
         if(t >= i) {
             t -= i;
             vis[i] = ;
             cnt1++;
         }
     }
     printf("%d\n", cnt1 * (n - cnt1));
     for(int i = ; i <= n; i++) {
         if(vis[i]) {
             for(int j = ; j <= n; j++) {
                 if(!vis[j]) {
                     printf("%d %d \n", i, j);
                 }
             }
         }
     }

     return ;
 }

AC代码

T3 题意：给定简单无向连通图，问是否能把所有边分成三个环。点可以重复经过。10w，10w，2s。

解：这TM居然是分类讨论...首先有度数为奇的肯定不行。然后只要排除一种情况：总环数 < 3即可。

因为如果环比较多，任意两个相邻(共用某一点)的环肯定能合二为一的......

如果有某个点的度数大于4，肯定合法。如果没有点的度数大于2，肯定不合法。

当点的度数最大为4的时候，可以把其他所有度数为2的点缩成某些边。

如果只有一个点的度数为4，相当于该点有两条自环，不行。

如果有两个点的度数为4，有一种特殊情况不合法：

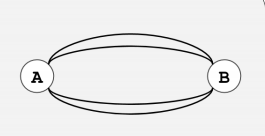
其余情况和有大于2个点的度数等于4的时候，均合法。

 #include <bits/stdc++.h>

 const int N = ;

 struct Edge {
     int nex, v;
 }edge[N << ]; int tp = ;

 int e[N], n, m, in[N], vis[N], stk[N], top, cnt, A, B;

 inline void add(int x, int y) {
     tp++;
     edge[tp].v = y;
     edge[tp].nex = e[x];
     e[x] = tp;
     return;
 }

 void DFS(int x, int f) {
     if(f && x == A) {
         puts("Yes");
         exit();
     }
     else if(x == B) return;
     for(int i = e[x]; i; i = edge[i].nex) {
         int y = edge[i].v;
         if(y != f) DFS(y, x);
     }
     return;
 }

 int main() {
     scanf("%d%d", &n, &m);
     for(int i = , x, y; i <= m; i++) {
         scanf("%d%d", &x, &y);
         add(x, y);
         add(y, x);
         in[x]++;
         in[y]++;
     }
     int largeIn = , cnt = ;
     for(int i = ; i <= n; i++) {
         if(in[i] & ) {
             puts("No");
             return ;
         }
         if(largeIn < in[i]) {
             largeIn = in[i];
             cnt = ;
         }
         else if(largeIn == in[i]) {
             cnt++;
         }
     }
     if(largeIn > ) {
         puts("Yes");
         return ;
     }
     else if(largeIn ==  && cnt > ) {
         puts("Yes");
         return ;
     }
     else if(largeIn ==  && cnt == ) {
         for(int i = ; i <= n; i++) {
             if(in[i] == ) {
                 if(!A) A = i;
                 else {
                     B = i;
                     break;
                 }
             }
         }
         DFS(A, );
     }
     puts("No");
     return ;
 }

AC代码

T4 题意：给定一个排列。你可以花费A使一个区间最左边的数跑到最右边，其余区间内的数左移。也可以花费B来进行逆操作。求使其变成升序的最小代价。5000,2s。

解：神仙DP。

显然有个n³的区间DP是设f[l][r]表示把[l, r]这一段排序。转移的时候一段区间可以由两个子区间拼起来，也可以找到其中最值然后挪一次。

正解全然不同......我们只注重这些元素的相对位置，也就是说下标可以为实数。

然后考虑每次操作等价于把一个数往旁边挪，别的数不变。

然后考虑最优解肯定是若干个数往左，若干个数往右，若干个数不动。我们以那些不动的数来DP。

设f[i][j]表示值域前i个数全部排好序了，且最大的那个不动的数是j，且比j大的数全部聚集在(j, j + 1)这一段的最小代价。

考虑f[i][j]是怎么得来的：如果当前这个数i初始时在j的左边，那么一定要往右移(i比j大)。反之一定要往左移(聚集到(j, j + 1)中)。

然后我们忽了一种转移：i在j右边的时候也可以不移动！此时f[i][i] = f[i - 1][j]

然后就完事了。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 LL f[N][N];
 int a[N], p[N];

 int main() {

     int n;
     LL A, B;
     scanf("%d%lld%lld", &n, &A, &B);
     for(int i = ; i <= n; i++) {
         scanf("%d", &a[i]);
         p[a[i]] = i;
     }
     memset(f, 0x3f, sizeof(f));
     /// DP
     f[][] = ;
     for(int i = ; i <= n; i++) {
         for(int j = ; j < i; j++) {
             /// f[i][j]
             /*for(int k = 0; k < i; k++) {
                 /// f[i][j] <- f[i - 1][k]
                 if(p[i] < p[k]) {
                     f[i][j] = std::min(f[i][j], f[i - 1][k] + A);
                 }
                 else {
                     f[i][j] = std::min(f[i][j], f[i - 1][k] + B);
                 }
             }*/
             if(p[i] < p[j]) {
                 f[i][j] = f[i - ][j] + A;
             }
             else {
                 f[i][j] = f[i - ][j] + B;
                 f[i][i] = std::min(f[i][i], f[i - ][j]);
             }
         }
         /*for(int j = 0; j <= i; j++) {
             printf("%3lld ", f[i][j]);
         }
         puts("");*/
     }

     LL ans = 4e18;
     for(int i = ; i <= n; i++) {
         ans = std::min(ans, f[n][i]);
     }
     printf("%lld\n", ans);
     return ;
 }

AC代码

T5 题意：给定序列，把它们两两配对使得每一对的和 % MO的最大值最小。10w,1e9,2s。

解：排序之后考虑最优方案长什么样。

然后发现它们一定长这样...因为不满足这样的方案调整成这样一定更优。

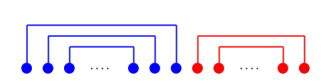
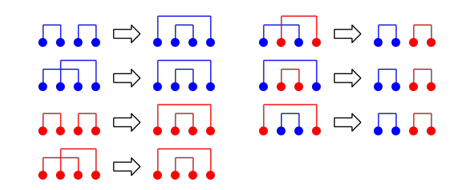
枚举分界点是n²的，但是发现分界点越靠左越优，于是二分这个分界点，使其满足条件(左边的和全小于MO，右边全不小于MO)，然后一次得出答案。

单调性：就考虑若分界点在a和b都满足条件，那么a，b之间的任一点也满足条件。比b小所以左边满足，比a大所以右边满足。

 #include <bits/stdc++.h>

 const int N = ;

 int a[N], MO, n;

 inline bool check(int p) {
     int l = p + , r = n;
     while(l < r) {
         if(a[l] + a[r] < MO) return false;
         l++;
         r--;
     }
     return true;
 }

 int main() {
     scanf("%d%d", &n, &MO);
     n <<= ;
     for(int i = ; i <= n; i++) {
         scanf("%d", &a[i]);
     }
     std::sort(a + , a + n + );

     int l = n, r = n; /// [1, l] (l, r]
     while(a[n] + a[l - ] >= MO && l >= ) l -= ;
     while(a[] + a[r] >= MO && r >= ) r -= ;
     l /= ;
     r /= ;

     while(l < r) {
         int mid = (l + r) >> ;
         if(check(mid * )) r = mid;
         else l = mid + ;
     }

     int p = r * ;
     int ans = ;
     l = , r = p;
     while(l < r) {
         ans = std::max(ans, a[l] + a[r]);
         l++;
         r--;
     }
     l = p + , r = n;
     while(l < r) {
         ans = std::max(ans, (a[l] + a[r]) % MO);
         l++;
         r--;
     }
     printf("%d\n", ans);
     return ;
 }

AC代码