对比Dijakstra和优先队列式分支限界

Dijakstra和分支限界都是基于广度优先搜索，如果说两者都是生成一棵树，那Dijakstra总是找距离树根最近的（属于贪心算法），优先队列式分支限界是在层遍历整棵搜索树的同时剪去达不到最优的树枝。

以下图为例：求从点s到点t的最短路径

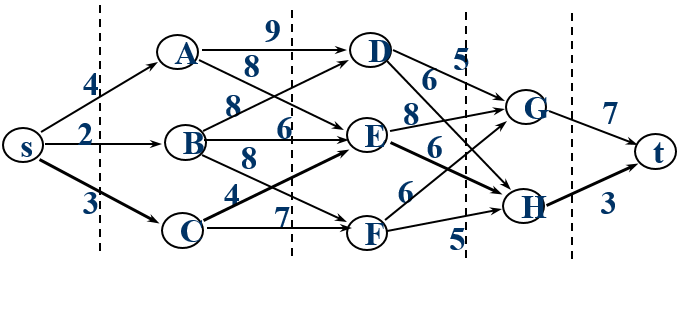
1. Dijakstra

第一步：初始化：将起点s加入集合S，并对所有非集合S的点的距离dist进行初始化（若不与s邻接，距离为无穷大）

第二步：在非集合S的点集合中，寻找离点s最近的点B（argmin dist[i]）并加入集合S，并对所有与B邻接且非集合S的点i的距离dist进行更新（若dist[i]>dist[B]+W[B][i] 则dist[i]=dist[B]+W[B][i]）

第三步：重复第二步，直到在非集合S的点集合中，找不到离点s的距离为有限值的点（这说明存在多棵生成树）。

主程序如下

while(1){
        x = FindShortest(Graph, collected);
        if(x == -1) break;
        collected[x] = 1;
        for(int i = 0;i<Graph->Nv;i++){
            if(!collected[i] && Graph->L[x][i] != INFINITY){
                if(dist[i] > dist[x] + Graph->L[x][i]){
                    dist[i] = dist[x] + Graph->L[x][i];
                    pri[i] = pri[x] + Graph->P[x][i];
                }
            }
        }
    }

2. 优先队列式分支限界法

分支限界法有队列式和优先队列式，两者区别在于，队列式只是单纯地满足先进先出，从而实现广度有限搜索，而优先队列式是对结点按目标函数值插入一个最大（小）堆，优先处理目标函数值较大（小）的结点。

解决单源最短路径的步骤：

第一步：初始化，将起点s加入优先队列（优先队列的目标函数值为距离dist，建立最小堆），并对所有非集合S的点的距离dist进行初始化（若不与s邻接，距离为无穷大）

第二步：从优先队列中取出点，对其所有邻接结点遍历，并对距离dist进行更新（若dist[i]>dist[B]+W[B][i]     则dist[i]=dist[B]+W[B][i]，并将其加入优先队列）

第三步：重复第二步，直到队列为空。

主程序如下（哈哈..这个不是我写的，看看就好）

while (true) {
     for (int j = 1; j <= n; j++)
       if ((c[E.i][j]<inf)&&(E.length+c[E.i][j]<dist[j])) {
         // 顶点i到顶点j可达，且满足控制约束
         dist[j]=E.length+c[E.i][j];
         prev[j]=E.i;
         // 加入活结点优先队列
         MinHeapNode<Type> N;
         N.i=j;
         N.length=dist[j];
         H.Insert(N);}
     try {H.DeleteMin(E);}         // 取下一扩展结点
     catch (OutOfBounds) {break;}  // 优先队列空
     }
} 

需要注意的是：在第二步中，若不满足条件dist[i]>dist[B]+W[B][i]，则不会对距离进行更新，也不会将其加入优先队列，这相当于对一个二叉搜索树的树枝进行了剪枝

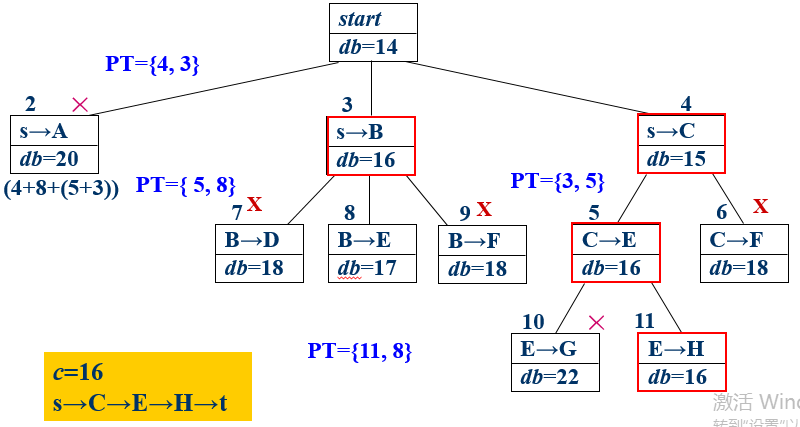
比如对s的邻接点进行遍历后，得到队列为BCA；然后对结点B的邻接点进行遍历，得到队列CAEDF；然后对结点C的邻接点进行遍历，首先是结点E，由于当前dist[E]>dist[C]+W[C][E]，E被加入优先队列，且排在上一个E之前，即AE1EDF，而F由于不满足条件，不会被再次加入优先队列；同样地，当对A进行遍历时，由于不满足条件，没有新的结点加入优先队列（相当于被剪枝），此时队列里有  E1EDF，依次进行下去....得到树如下图。

图里的db可以忽略。。。反正真正跑程序也不会去计算所谓的限界值。