MT【253】仿射和蒙日圆
如图,设点$M(x_0,y_0)$是椭圆$C:\dfrac{x^2}{2}+y^2=1$上一点,从原点$O$向圆$M:(x-x_0)^2+(y-y_0)^2=\dfrac{2}{3}$作两条切线分别与椭圆$C$交于$P,Q$,直线$OP,OQ$的斜率分别为$k_1,k_2$
(1)求证:$k_1k_2$为定值
(2)求四边形$OPQM$面积的最大值.
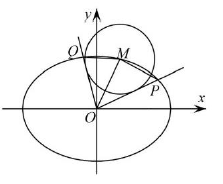

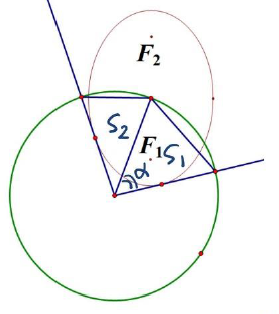
分析:涉及到面积最大容易想到仿射变换:
(1)
$$\begin{cases}
x^{'}&=x\\
y^{'}&=\sqrt{2}y
\end{cases}$$
则$k^{'}=\sqrt{2}k$,由蒙日圆性质得$k_1^{'}k_2^{'}=-1$故$k_1k_2=-\dfrac{1}{2}$
(2)如图$S=\dfrac{1}{\sqrt{2}}(S_1+S_2)=\dfrac{1}{\sqrt{2}}(sin\alpha+cos\alpha)\le1$
第二小问常规方法提示:

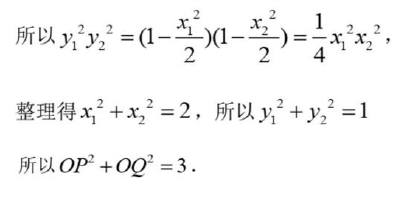
MT【253】仿射和蒙日圆的更多相关文章
- MT【290】内外圆求三角最值
求$\sqrt{\dfrac{5}{4}-\sin x}+2\sqrt{\dfrac{9}{4}+\cos x-\sin x}$的最小值. 提示:$\sqrt{\dfrac{5}{4}-\sin x} ...
- MT【32】内外圆(Apollonius Circle)的几何证明
另一方面,如果 M 满足(1)式,那么M必然在以PQ为直径的圆上.事实上当M为P或者Q时,这是显然的.当M异于P,Q时,由$\frac{|MB|}{|MC|}=\frac{|PB|}{|PC|}=\l ...
- MT【172】内外圆
$P,Q$是两个定点,M为平面内一个动点,且$\dfrac{|MP|}{|MQ|}=\lambda(\lambda>0,\lambda\ne1)$, 点M的轨迹围成的区域面积为S , 设$S=f ...
- MT【210】四点共圆+角平分线
(2018全国联赛解答最后一题)在平面直角坐标系$xOy$中,设$AB$是抛物线$y^2=4x$的过点$F(1,0)$的弦,$\Delta{AOB}$的外接圆交抛物线于点$P$(不同于点$A,O,B$ ...
- MT【306】圆与椭圆公切线段
已知椭圆方程$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$,圆方程$x^2+y^2=r^2,(3<r^2<4)$,若直线$l$与椭圆和圆分别切于点$P,Q$求$|PQ| ...
- MT【125】四点共圆
(2017湖南省高中数学竞赛16题) \(AB\)是椭圆\(mx^2+ny^2=1(m>0,n>0,m\ne n)\)的斜率为 1 的弦.\(AB\)的垂直平分线与椭圆交于两点\(CD\) ...
- MT【107】立体几何中用阿波罗尼乌斯圆的一道题
分析:利用内外圆知识知道,B,C两点到 AD 的距离$\le4$. 利用体积公式$V=\frac{1}{3}S_{截面}|AD|\le2\sqrt{15}$
- MT【191】阿波罗尼乌斯圆
已知$f(x)=2\sqrt{(\cos x+\frac{1}{2})^2+\sin^2 x}-\sqrt{\cos^2 x+(\sin x-\frac{1}{2})^2}$,若$m\ge f(x)$ ...
- C++ 2(将类分文件) //点和圆的关系 //设计一个圆形类 和一个点类 计算点和圆的关系 //点到圆心的距离 == 半径 点在圆上 //点到圆心的距离 > 半径 点在圆外 //点到圆心的距离 < 半径 点在圆内 //点到圆心的距离 获取 ....... (x1 -x2)^2 + (y1-y2)^2 开根号 和半径对比 // 计算 可以 两边同时 平方
1 源文件 main.cpp 2 //点和圆的关系 3 //设计一个圆形类 和一个点类 计算点和圆的关系 4 //点到圆心的距离 == 半径 点在圆上 5 //点到圆心的距离 > 半径 点在圆外 ...
随机推荐
- H5 id选择器和class选择器
11-id选择器和class选择器 第一段文字 第二段文字 第三段文字 --> 第一段文字 第二段文字 第三段文字 <!DOCTYPE html> <html lang=&qu ...
- CSS scroll-behavior属性: 滚动框指定滚动行为
概念 当用户手动导航或者 CSSOM scrolling API 触发滚动操作时,CSS 属性 scroll-behavior 为一个滚动框指定滚动行为,其他任何的滚动,例如那些由于用户行为而产生的滚 ...
- #Leetcode# 985. Sum of Even Numbers After Queries
https://leetcode.com/problems/sum-of-even-numbers-after-queries/ We have an array A of integers, and ...
- 08-webpack的介绍
在这里我仅仅的是对webpack做个讲解,webpack这个工具非常强大,解决了我们前端很繁琐的一些工具流程繁琐的事情.如果感兴趣的同学,简易还是看官网吧. 中文链接地址:https://www.we ...
- 父级div宽度100%,子级一个div宽度固定,另一个宽度自适应
<!DOCTYPE html> <html> <head> <title>布局测试</title> <style type=" ...
- 文件传输协议FTP、SFTP和SCP
网络通信协议分层 应用层: HTTP(Hypertext Transfer Protocol 超文本传输协议,显示网页) DNS(Domain Name System) FTP(File Transf ...
- myecplise ssh项目配置上遇到的问题
版本:spring3.1+hib4.1+struts2.1 学习项目使用此版本运行时,总是会遇到各样的错误,在这里做一下记录. 问题1:log4j相关 spring的web项目,执行时报错: 信息: ...
- vue单页面模板说明文档(1)
Introduction This boilerplate is targeted towards large, serious projects and assumes you are somewh ...
- mybatis数据源与连接池
1.概念介绍1.1 数据源:顾名思义,数据的来源,它包含了数据库类型信息,位置和数据等信息,一个数据源对应一个数据库. 1.2 连接池:在做持久化操作时,需要通过数据库连接对象来连接数据库,而连接池就 ...
- 区分Python中的可变对象和不可变对象
参考: https://www.cnblogs.com/sun-haiyu/p/7096918.html """不过注意函数传参既不是传值也不是传引用,正确的叫法是传对象 ...
