数学图形之贝塞尔(Bézier)曲面

前面章节中讲了贝塞尔(Bézier)曲线,而贝塞尔曲面是对其多一个维度的扩展.其公式依然是曲线的公式:

。

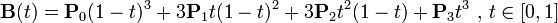而之所以由曲线变成曲面,是将顶点横向连了再纵向连.

很多计算机图形学的教程都会有贝塞尔曲面的DEMO.而这里,我依然是使用我制定的脚本代码生成贝塞尔曲面.代码中的控制顶点坐标为随机数生成,所以每次生成的曲面图形都不一样.

相关软件参见:数学图形可视化工具,使用自己定义语法的脚本代码生成数学图形.该软件免费开源.QQ交流群: 367752815

二次贝塞尔曲面:

需要生成3*3个控制顶点

vertices = D1: D2:

u = from  to  D1
v = from  to  D2

ax0 = rand2(-, )
ay0 = rand2(-, )
az0 = rand2(-, )
bx0 = rand2(-, )
by0 = rand2(-, )
bz0 = rand2(-, )
cx0 = rand2(-, )
cy0 = rand2(-, )
cz0 = rand2(-, )

ax1 = rand2(-, )
ay1 = rand2(-, )
az1 = rand2(-, )
bx1 = rand2(-, )
by1 = rand2(-, )
bz1 = rand2(-, )
cx1 = rand2(-, )
cy1 = rand2(-, )
cz1 = rand2(-, )

ax2 = rand2(-, )
ay2 = rand2(-, )
az2 = rand2(-, )
bx2 = rand2(-, )
by2 = rand2(-, )
bz2 = rand2(-, )
cx2 = rand2(-, )
cy2 = rand2(-, )
cz2 = rand2(-, )

ax3 = rand2(-, )
ay3 = rand2(-, )
az3 = rand2(-, )
bx3 = rand2(-, )
by3 = rand2(-, )
bz3 = rand2(-, )
cx3 = rand2(-, )
cy3 = rand2(-, )
cz3 = rand2(-, )

u1 = (-u)*(-u)
u2 = *(-u)*u
u3 = u*u

ax = u1*ax0+u2*ax1+u3*ax2
ay = u1*ay0+u2*ay1+u3*ay2
az = u1*az0+u2*az1+u3*az2
bx = u1*bx0+u2*bx1+u3*bx2
by = u1*by0+u2*by1+u3*by2
bz = u1*bz0+u2*bz1+u3*bz2
cx = u1*cx0+u2*cx1+u3*cx2
cy = u1*cy0+u2*cy1+u3*cy2
cz = u1*cz0+u2*cz1+u3*cz2

v1 = (-v)*(-v)
v2 = *(-v)*v
v3 = v*v

x = v1*ax+v2*bx+v3*cx
y = v1*ay+v2*by+v3*cy
z = v1*az+v2*bz+v3*cz

u = u*
v = v*

三次贝塞尔曲面:

需要生成4*4个控制顶点

vertices = D1: D2:

u = from  to  D1
v = from  to  D2

ax0 = rand2(-, )
ay0 = rand2(-, )
az0 = rand2(-, )
bx0 = rand2(-, )
by0 = rand2(-, )
bz0 = rand2(-, )
cx0 = rand2(-, )
cy0 = rand2(-, )
cz0 = rand2(-, )
dx0 = rand2(-, )
dy0 = rand2(-, )
dz0 = rand2(-, )

ax1 = rand2(-, )
ay1 = rand2(-, )
az1 = rand2(-, )
bx1 = rand2(-, )
by1 = rand2(-, )
bz1 = rand2(-, )
cx1 = rand2(-, )
cy1 = rand2(-, )
cz1 = rand2(-, )
dx1 = rand2(-, )
dy1 = rand2(-, )
dz1 = rand2(-, )

ax2 = rand2(-, )
ay2 = rand2(-, )
az2 = rand2(-, )
bx2 = rand2(-, )
by2 = rand2(-, )
bz2 = rand2(-, )
cx2 = rand2(-, )
cy2 = rand2(-, )
cz2 = rand2(-, )
dx2 = rand2(-, )
dy2 = rand2(-, )
dz2 = rand2(-, )

ax3 = rand2(-, )
ay3 = rand2(-, )
az3 = rand2(-, )
bx3 = rand2(-, )
by3 = rand2(-, )
bz3 = rand2(-, )
cx3 = rand2(-, )
cy3 = rand2(-, )
cz3 = rand2(-, )
dx3 = rand2(-, )
dy3 = rand2(-, )
dz3 = rand2(-, )

u1 = pow((-u),)
u2 = *pow((-u),)*u
u3 = *u*u*(-u)
u4 = u*u*u

ax = u1*ax0+u2*ax1+u3*ax2+u4*ax3
ay = u1*ay0+u2*ay1+u3*ay2+u4*ay3
az = u1*az0+u2*az1+u3*az2+u4*az3
bx = u1*bx0+u2*bx1+u3*bx2+u4*bx3
by = u1*by0+u2*by1+u3*by2+u4*by3
bz = u1*bz0+u2*bz1+u3*bz2+u4*bz3
cx = u1*cx0+u2*cx1+u3*cx2+u4*cx3
cy = u1*cy0+u2*cy1+u3*cy2+u4*cy3
cz = u1*cz0+u2*cz1+u3*cz2+u4*cz3
dx = u1*dx0+u2*dx1+u3*dx2+u4*dx3
dy = u1*dy0+u2*dy1+u3*dy2+u4*dy3
dz = u1*dz0+u2*dz1+u3*dz2+u4*dz3

v1 = pow((-v),)
v2 = *pow((-v),)*v
v3 = *v*v*(-v)
v4 = v*v*v

x = v1*ax+v2*bx+v3*cx+v4*dx
y = v1*ay+v2*by+v3*cy+v4*dy
z = v1*az+v2*bz+v3*cz+v4*dz

u = u*
v = v*