Maximum repetition substring 后缀数组
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 7578 | Accepted: 2281 |
Description
The repetition number of a string is defined as the maximum number R such that the string can be partitioned into R same consecutive substrings. For example, the repetition number of "ababab" is 3 and "ababa" is 1.
Given a string containing lowercase letters, you are to find a substring of it with maximum repetition number.
Input
The input consists of multiple test cases. Each test case contains exactly one line, which gives a non-empty string consisting of lowercase letters. The length of the string will not be greater than 100,000.
The last test case is followed by a line containing a '#'.
Output
For each test case, print a line containing the test case number( beginning with 1) followed by the substring of maximum repetition number. If there are multiple substrings of maximum repetition number, print the lexicographically smallest one.
Sample Input
ccabababc
daabbccaa
#
Sample Output
Case 1: ababab
Case 2: aa
Source


#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <list>
#include <iomanip>
#include <cstdlib>
using namespace std;
const int INF=0x5fffffff;
const double EXP=1e-;
const int MS=;
// KMP TRIE DFA SUFFIX
int dp[MS][]; // RMQ
int t1[MS],t2[MS],c[MS],v[MS];
int rank[MS],sa[MS],height[MS];
char str[MS],str1[MS];
int s[MS];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
} void get_sa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=t1,*y=t2;
for(i=;i<m;i++)
c[i]=;
for(i=;i<n;i++)
c[x[i]=r[i]]++;
for(i=;i<m;i++)
c[i]+=c[i-];
for(i=n-;i>=;i--)
sa[--c[x[i]]]=i;
p=;j=;
for(;p<n;j*=,m=p)
{
for(p=,i=n-j;i<n;i++)
y[p++]=i;
for(i=;i<n;i++)
if(sa[i]>=j)
y[p++]=sa[i]-j;
for(i=;i<n;i++)
v[i]=x[y[i]];
for(i=;i<m;i++)
c[i]=;
for(i=;i<n;i++)
c[v[i]]++;
for(i=;i<m;i++)
c[i]+=c[i-];
for(i=n-;i>=;i--)
sa[--c[v[i]]]=y[i];
swap(x,y);
x[sa[]]=;
for(p=,i=;i<n;i++)
x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;
}
} void get_height(int *r,int n)
{
int i,j,k=;
for(i=;i<=n;i++)
rank[sa[i]]=i;
//height[i]>=height[i-1]-1;
for(i=;i<n;i++)
{
if(k)
k--;
else
k=;
j=sa[rank[i]-];
while(r[i+k]==r[j+k])
k++;
height[rank[i]]=k;
}
} void rmq_init(int n)
{
for(int i=;i<=n;i++) dp[i][]=height[i];
for(int j=;(<<j)<=n;j++)
for(int i=;i+(<<j)-<=n;i++)
dp[i][j]=min(dp[i][j-],dp[i+(<<(j-))][j-]);
} int rmq(int ll,int rr)
{
int k=;
ll=rank[ll];
rr=rank[rr];
if(ll>rr)
{
int tmp=ll;
ll=rr;
rr=tmp;
}
ll++;
while((<<(k+))<=rr-ll+) k++;
return min(dp[ll][k],dp[rr-(<<k)+][k]);
} int main()
{
int text=;
while(scanf("%s",str)>)
{
if(str[]=='#')
break;
int len=strlen(str);
for(int i=;i<len;i++)
s[i]=str[i]-'a'+;
s[len]=;
get_sa(s,sa,len+,);
get_height(s,len);
rmq_init(len);
int ans=,pos=,lenn;
for(int i=;i<=len/;i++)
{
for(int j=;j<len-i;j+=i)
{
if(str[j]!=str[j+i])
continue;
int k=rmq(j,j+i);
int tol=k/i+;
//printf("%d\n",tol);
int r=i-k%i;
int p=j;
int cnt=;
for(int m=j-;m>j-i&&str[m]==str[m+i]&&m>=;m--)
{
cnt++;
if(cnt==r)
{
tol++;
p=m;
}
else if(rank[p]>rank[m])
{
p=m;
}
}
if(ans<tol)
{
ans=tol;
pos=p;
lenn=tol*i;
}
else if(ans==tol&&rank[pos]>rank[p])
{
pos=p;
lenn=tol*i;
}
}
}
printf("Case %d: ",++text);
// printf("%d %d %d\n",ans,pos,lenn);
if(ans<) //这里,如果字符总长度小于2,那么就在原串中找出一个最小的字符就好
{
char ch='z';
for(int i=;i<len;i++)
if(str[i]<ch)
ch=str[i];
printf("%c\n",ch);
continue;
}
for(int i=pos;i<pos+lenn;i++)
printf("%c",str[i]);
printf("\n");
}
return ;
}
Maximum repetition substring 后缀数组的更多相关文章
- POJ3693 Maximum repetition substring [后缀数组 ST表]
Maximum repetition substring Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 9458 Acc ...
- POJ3693 Maximum repetition substring 后缀数组
POJ - 3693 Maximum repetition substring 题意 输入一个串,求重复次数最多的连续重复字串,如果有次数相同的,则输出字典序最小的 Sample input ccab ...
- POJ3693 Maximum repetition substring —— 后缀数组 重复次数最多的连续重复子串
题目链接:https://vjudge.net/problem/POJ-3693 Maximum repetition substring Time Limit: 1000MS Memory Li ...
- poj3693 Maximum repetition substring (后缀数组+rmq)
Description The repetition number of a string is defined as the maximum number R such that the strin ...
- POJ 3693 Maximum repetition substring ——后缀数组
重复次数最多的字串,我们可以枚举循环节的长度. 然后正反两次LCP,然后发现如果长度%L有剩余的情况时,答案是在一个区间内的. 所以需要找到区间内最小的rk值. 两个后缀数组,四个ST表,$\Thet ...
- 【Poj-3693】Maximum repetition substring 后缀数组 连续重复子串
POJ - 3693 题意 SPOJ - REPEATS的进阶版,在这题的基础上输出字典序最小的重复字串. 思路 跟上题一样,先求出最长的重复次数,在求的过程中顺便纪录最多次数可能的长度. 因为sa数 ...
- poj 3693 Maximum repetition substring (后缀数组)
其实是论文题.. 题意:求一个字符串中,能由单位串repeat得到的子串中,单位串重复次数最多的子串.若有多个重复次数相同的,输出字典序最小的那个. 解题思路:其实跟论文差不多,我看了很久没看懂,后来 ...
- POJ 3693 Maximum repetition substring (后缀数组+RMQ)
题意:给定一个字符串,求其中一个由循环子串构成且循环次数最多的一个子串,有多个就输出最小字典序的. 析:枚举循环串的长度ll,然后如果它出现了两次,那么它一定会覆盖s[0],s[ll],s[ll*2] ...
- POJ-3693-Maximum repetition substring(后缀数组-重复次数最多的连续重复子串)
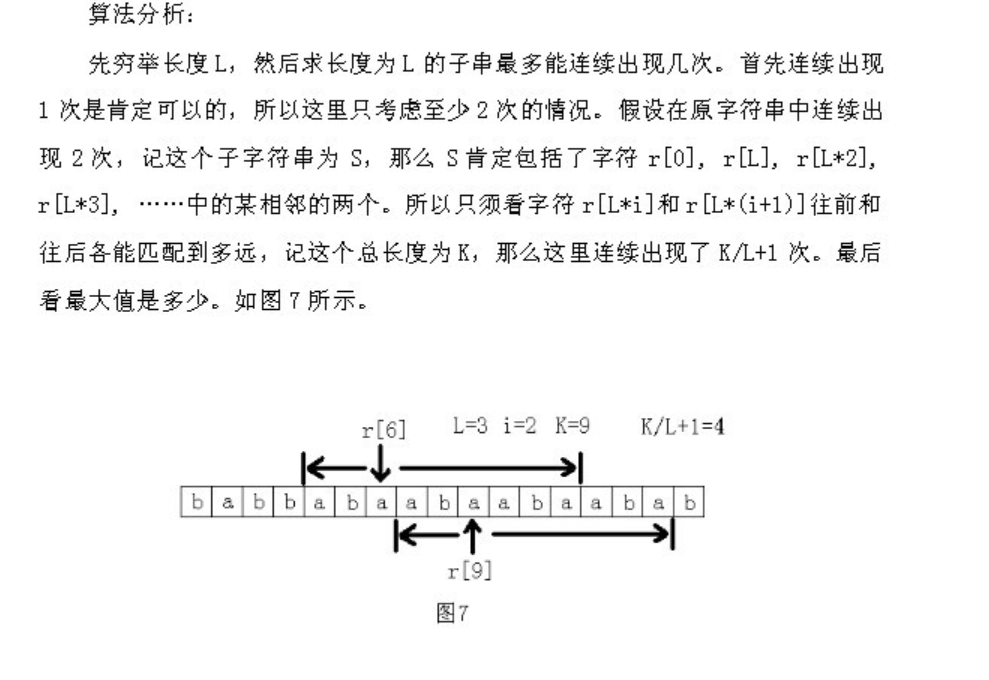
题意: 给出一个串,求重复次数最多的连续重复子串 分析: 比较容易理解的部分就是枚举长度为L,然后看长度为L的字符串最多连续出现几次. 既然长度为L的串重复出现,那么str[0],str[l],str ...
随机推荐
- 第三百二十八天 how can I 坚持
今天电脑快把我搞疯了,一天得死机快十次,不知道怎么回事,最后升级了win10,感觉就是比较好. 哎,成了这个样子,当初为什么又让我抽中了那个签,搞不懂啊,这都是为啥. 我哪里错了,还是冥冥中自有天意, ...
- 解决Ubuntu系统的每次开机重启后,resolv.conf清空的问题
问题情况描述如下: 普及知识: /etc/resolv.conf ,其实是一个Link .它其实指向的是 /run/resolvconf/resolv.conf. Ubuntu 有一个 reso ...
- java反射工具类
package com.yingchao.kgou.core; import java.lang.reflect.Field; import java.lang.reflect.InvocationT ...
- 用vagrant搭建一个自己的lnmp环境(一)
用vagrant搭建自己的lnmp环境 1.工具: a.vagrant b.virtual box c.linux服务器box(此处我使用centos 7.0) 2.安装完vagrant和virtua ...
- 利用HTML5开发Android(6)---构建HTML5离线应用
需要提供一个cache manifest文件,理出所有需要在离线状态下使用的资源例如 Manifest代码 CACHE MANIFEST #这是注释 images/sound-icon.png ima ...
- [转]Kerberos简介
Kerberos协议: Kerberos协议主要用于计算机网络的身份鉴别(Authentication), 其特点是用户只需输入一次身份验证信息就可以凭借此验证获得的票据(ticket-grantin ...
- spring4 定时任务
一.spring 定时任务 spring 定时任务 ,最好使用quartz 实现.下面我以spring4为例 二.实战(默认) 1.pom配置 <!-- spring time task --& ...
- vs2010代码注释自动生成api文档
最近做了一些接口,提供其他人调用,要写个api文档,可是我想代码注释已经写了说明,能不能直接把代码注释生成api?于是找到以下方法 环境:vs2010 先下载安装Sandcastle 和Sandcas ...
- RDD的依赖关系
RDD的依赖关系 Rdd之间的依赖关系通过rdd中的getDependencies来进行表示, 在提交job后,会通过在DAGShuduler.submitStage-->getMissingP ...
- Effective C++ Item 37 绝不又一次定义继承而来的缺省參数值
本文为senlie原创,转载请保留此地址:http://blog.csdn.net/zhengsenlie 经验:绝对不要又一次而来的缺省參数值.由于缺省參数值都是静态绑定,而 virtual 函数 ...
