POJ 1661 Help Jimmy -- 动态规划

题目地址：http://poj.org/problem?id=1661

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。




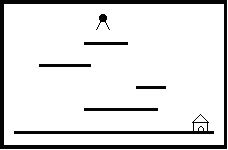
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。



Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。



设计一个程序，计算Jimmy到底地面时可能的最早时间。

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <=
20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。



Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

Source

POJ Monthly--2004.05.15 CEOI 2000

当Jimmy落在一个平台上后有两种选择（向左走或向右走），而Jimmy走到平台左边和右边的时间很容易计算，如果我们得到了以平台左边为起点及以平台右边为起点到地面的最短时间，那么选择往左走还是往右走就很容易了。这样，原问题就分解为两个子问题这两个子问题和原问题的形式是一致的了，也就找到了“状态”dp[i][j], j = 0, 1 (dp[i][0]表示以i号平台左边为起点到地面的最短时间，dp[i][1]]表示以i号平台右边为起点到地面的最短时间)，而“状态转移方程”如下：

dp[i][0] = H[i] - H[m] + Min (dp[m][0] + X1[i] - X1[m], dp[m][1] + X2[m] - X1[i]);  m为i左边下面的平台的编号

dp[i][1] = H[i] - H[m] + Min (dp[m][0] + X2[i] - X1[m], dp[m][1] + X2[m] - X2[i]);  m为i右边下面的平台的编号

算法实现如下：

#include <stdio.h>
#include <stdlib.h>

#define MAXN 1010
#define INF 9000000

typedef struct platform{
	int x1;
	int x2;
	int high;
}Platform;

int compare (const void * p, const void * q){
	Platform * p1 = (Platform *)p;
	Platform * q1 = (Platform *)q;
	return p1->high - q1->high;
}

int Min (int a, int b){
	return (a < b) ? a : b;
}

int N, X, Y, MAX;
Platform plat[MAXN];
int dp[MAXN][2];         //dp[i][0]、dp[i][1]分别表示从第i个平台左、右边到地面的最短时间

void LeftMinTime (int i){    //计算从平台i左边到地面的最短时间
	int k = i - 1;
	while (k > 0 && plat[i].high - plat[k].high <= MAX){
		//如果平台i左边下面有平台，且两者相距不超过MAX
		if (plat[i].x1 >= plat[k].x1 && plat[i].x1 <= plat[k].x2){
			dp[i][0] = plat[i].high - plat[k].high +
				Min (plat[i].x1 - plat[k].x1 + dp[k][0], plat[k].x2 - plat[i].x1 + dp[k][1]);
			return;
		}
		else
			--k;
	}
	//如果平台i左边下面没有平台，或者两者相距超过了MAX
	if (plat[i].high - plat[k].high > MAX)
		dp[i][0] = INF;
	else
		dp[i][0] = plat[i].high;
}

void RightMinTime (int i){   //计算从平台i右边到地面的最短时间
	int k = i - 1;
	while (k > 0 && plat[i].high - plat[k].high <= MAX){
		//如果平台i右边下面有平台，且两者相距不超过MAX
		if (plat[i].x2 >= plat[k].x1 && plat[i].x2 <= plat[k].x2){
			dp[i][1] = plat[i].high - plat[k].high +
				Min (plat[i].x2 - plat[k].x1 + dp[k][0], plat[k].x2 - plat[i].x2 + dp[k][1]);
			return;
		}
		else
			--k;
	}
	//如果平台i右边下面没有平台，或者两者相距超过了MAX
	if (plat[i].high - plat[k].high > MAX)
		dp[i][1] = INF;
	else
		dp[i][1] = plat[i].high;
}

int ShortestTime (){
	int i, j;

	for (i=1; i<=N+1; ++i){
		LeftMinTime (i);
		RightMinTime (i);
	}
	return Min (dp[N+1][0], dp[N+1][1]);
}

int main(void){
	int t;
	int i;
	while (scanf ("%d", &t) != EOF){
		while (t-- != 0){
			scanf ("%d%d%d%d", &N, &X, &Y, &MAX);
			for (i=1; i<=N; ++i){
				scanf ("%d%d%d", &plat[i].x1, &plat[i].x2, &plat[i].high);
			}
			plat[0].high = 0;
			plat[0].x1 = -20000;
			plat[0].x2 = 20000;
			plat[N+1].high = Y;
			plat[N+1].x1 = X;
			plat[N+1].x2 = X;
			//根据平台高度按从低到高排序
			qsort (plat, N+2, sizeof(Platform), compare);
			printf ("%d\n", ShortestTime());
		}
	}

	return 0;
}

参考资料：http://blog.csdn.net/alalalalalqp/article/details/9206299