决策树--信息增益，信息增益比，Geni指数的理解

决策树 是表示基于特征对实例进行分类的树形结构

      从给定的训练数据集中，依据特征选择的准则，递归的选择最优划分特征，并根据此特征将训练数据进行分割，使得各子数据集有一个最好的分类的过程。

 

决策树算法3要素：

• • 特征选择
  • 决策树生成
  • 决策树剪枝

 

部分理解：

 

关于决策树生成

决策树的生成过程就是 使用满足划分准则的特征不断的将数据集划分为纯度更高，不确定性更小的子集的过程。

对于当前数据集D的每一次的划分，都希望根据某特征划分之后的各个子集的纯度更高，不确定性更小。

 

而如何度量划分数据集前后的数据集的纯度以及不确定性呢？ 

   答案：特征选择准则，比如：信息增益，信息增益率，基尼指数

 

特征选择准则：

目的：使用某特征对数据集划分之后，各数据子集的纯度要比划分前的数据集D的纯度高（不确定性要比划分前数据集D的不确定性低。）

注意：

         1. 划分后的纯度为各数据子集的纯度的加和（子集占比*子集的经验熵）。

         2. 度量划分前后的纯度变化 用子集的纯度之和与划分前的数据集D的纯度 进行对比。

 

特征选择的准则就是 度量样本集合不确定性以及纯度的方法。本质相同，定义不同而已。

 

特征选择的准则主要有以下三种：信息增益，信息增益率，基尼指数

---

首先介绍一下熵的概念以及理解：

熵：度量随机变量的不确定性。（纯度）

定义：假设随机变量X的可能取值有x_1，x₂， ... , x_n

         对于每一个可能的取值x_i，其概率 P(X=x_i) = p_i , ( i = 1,2, ... , n)

         因此随机变量X的熵：

                                 

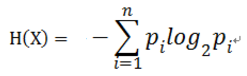
对于样本集合D来说，随机变量X是样本的类别，即，假设样本有k个类别，每个类别的概率是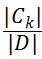，其中|C_k|表示类别k的样本个数，|D|表示样本总数

则对于样本集合D来说熵（经验熵）为：

---

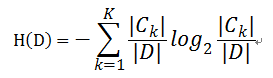
• 信息增益（ ID3算法 ）

定义： 以某特征划分数据集前后的熵的差值

在熵的理解那部分提到了，熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。

      划分前样本集合D的熵是一定的 ，entroy(前)，

      使用某个特征A划分数据集D，计算划分后的数据子集的熵 entroy(后)

                                   信息增益 =  entroy(前) -  entroy(后)

          书中公式:

做法：计算使用所有特征划分数据集D，得到多个特征划分数据集D的信息增益，从这些信息增益中选择最大的，因而当前结点的划分特征便是使信息增益最大的划分所使用的特征。

信息增益的理解：

               对于待划分的数据集D，其 entroy(前)是一定的，但是划分之后的熵 entroy(后)是不定的，entroy(后)越小说明使用此特征划分得到的子集的不确定性越小（也就是纯度越高），因此 entroy(前) -  entroy(后)差异越大，说明使用当前特征划分数据集D的话，其纯度上升的更快。而我们在构建最优的决策树的时候总希望能更快速到达纯度更高的集合，这一点可以参考优化算法中的梯度下降算法，每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值减小最快的方向。同理：在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展，因此我们总是选择使得信息增益最大的特征来划分当前数据集D。

 缺点：信息增益偏向取值较多的特征

       原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较 偏向取值较多的特征。

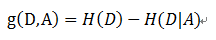
• 解决方法 :  信息增益比（ C4.5算法 ）

      信息增益比 = 惩罚参数 * 信息增益

书中公式：

       注意：其中的H_A(D)，对于样本集合D，将当前特征A作为随机变量（取值是特征A的各个特征值），求得的经验熵。

      （之前是把集合类别作为随机变量，现在把某个特征作为随机变量，按照此特征的特征取值对集合D进行划分，计算熵H_A(D)）

      信息增益比本质： 是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。

        惩罚参数：数据集D以特征A作为随机变量的熵的倒数，即：将特征A取值相同的样本划分到同一个子集中（之前所说数据集的熵是依据类别进行划分的）

        

        缺点：信息增益比偏向取值较少的特征   

        原因：  当特征取值较少时H_A(D)的值较小，因此其倒数较大，因而信息增益比较大。因而偏向取值较少的特征。

        使用信息增益比：基于以上缺点，并不是直接选择信息增益率最大的特征，而是现在候选特征中找出信息增益高于平均水平的特征，然后在这些特征中再选择信息增益率最高的特征。   

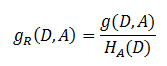
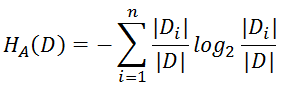
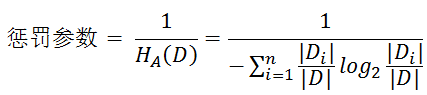
• 基尼指数（ CART算法 ---分类树）

定义：基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。

注意： Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。

即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

书中公式：

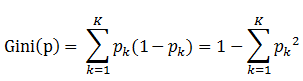
说明:

1. p_k表示选中的样本属于k类别的概率，则这个样本被分错的概率是(1-p_k)

2. 样本集合中有K个类别，一个随机选中的样本可以属于这k个类别中的任意一个，因而对类别就加和

3. 当为二分类是，Gini(P) = 2p(1-p)

样本集合D的Gini指数 ： 假设集合中有K个类别，则：

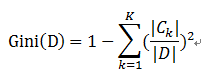
基于特征A划分样本集合D之后的基尼指数：

需要说明的是CART是个二叉树，也就是当使用某个特征划分样本集合只有两个集合：1. 等于给定的特征值 的样本集合D₁ ， 2 不等于给定的特征值 的样本集合D₂

实际上是对拥有多个取值的特征的二值处理。

举个例子：

假设现在有特征 “学历”，此特征有三个特征取值： “本科”，“硕士”， “博士”，

当使用“学历”这个特征对样本集合D进行划分时，划分值分别有三个，因而有三种划分的可能集合，划分后的子集如下：

1. 1. 划分点： “本科”，划分后的子集合 ： {本科}，{硕士，博士}
   2. 划分点： “硕士”，划分后的子集合 ： {硕士}，{本科，博士}
   3.     划分点： “硕士”，划分后的子集合 ： {博士}，{本科，硕士}

对于上述的每一种划分，都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度：

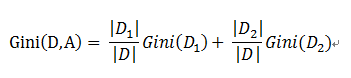
因而对于一个具有多个取值（超过2个）的特征，需要计算以每一个取值作为划分点，对样本D划分之后子集的纯度Gini(D,A_i)，(其中A_i 表示特征A的可能取值)

然后从所有的可能划分的Gini(D,A_i)中找出Gini指数最小的划分，这个划分的划分点，便是使用特征A对样本集合D进行划分的最佳划分点。