P2245 星际导航

题目描述

sideman 做好了回到 Gliese星球的硬件准备，但是 sideman 的导航系统还没有完全设计好。为了方便起见，我们可以认为宇宙是一张有 N 个顶点和 M 条边的带权无向图，顶点表示各个星系，两个星系之间有边就表示两个星系之间可以直航，而边权则是航行的危险程度。

sideman 现在想把危险程度降到最小，具体地来说，就是对于若干个询问 (A, B)，sideman 想知道从顶点 AA航行到顶点 B 所经过的最危险的边的危险程度值最小可能是多少。作为 sideman 的同学，你们要帮助 sideman返回家园，兼享受安全美妙的宇宙航行。所以这个任务就交给你了。

输入输出格式

输入格式：

第一行包含两个正整数 N 和 M，表示点数和边数。

之后 M 行，每行三个整数 A，B 和 L，表示顶点 A 和 B 之间有一条边长为 L 的边。顶点从 1 开始标号。

下面一行包含一个正整数 Q，表示询问的数目。

之后 Q 行，每行两个整数 A 和 B，表示询问 A 和 B 之间最危险的边危险程度的可能最小值。

输出格式：

对于每个询问， 在单独的一行内输出结果。如果两个顶点之间不可达， 输出 impossible。

输入输出样例

输入样例#1： 复制

4 5

1 2 5

1 3 2

2 3 11

2 4 6

3 4 4

3

2 3

1 4

1 2

输出样例#1： 复制

5

4

5

说明

对于 40% 的数据，满足 \(N \leq 1000, M \leq 3000, Q \leq 1000\)。

对于 80% 的数据，满足 \(N \leq 10000, M \leq 10^5, Q \leq 1000\)。

对于 100% 的数据，满足 \(N \leq 10^5, M \leq 3 \times 10^5, Q \leq 10^5, L \leq 10^9\)。数据不保证没有重边和自环。

---

kruskal重构树

在最小生成树时每次合并两个节点时把它们合并到一个新的点上，这个点的权值就是两点间边的权值

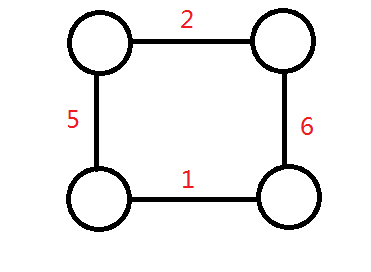
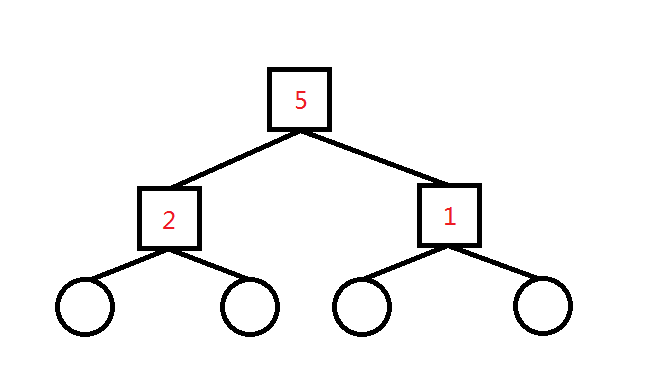
每两个点间的lca就是它们最小路径上的最大值

---

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define M 300010
#define LL long long
#define RI register int
#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))

using namespace std;

int m,n,j,k,a[M],ver[M],edge[M],head[M],nex[M],cnt,top[M],wson[M],f[M],s[M],d[M],x,y,z,father[M],cn;

struct vv
{
    int ver,edge,fr;
} v[M];

inline char gc()
{
    static char now[1<<22],*S,*T;
    if (T==S)
    {
        T=(S=now)+fread(now,1,1<<22,stdin);
        if (T==S) return EOF;
    }
    return *S++;
}
inline int gtt()
{
    register int x=0,f=1;
    register char ch=gc();
    while(!isdigit(ch))
    {
        if (ch=='-') f=-1;
        ch=gc();
    }
    while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-'0',ch=gc();
    return x*f;
}

inline void ptt(int a)
{
    RI b[100], k=a, g=0;
    while(k) b[++g]=k%10, k/=10;
    for(g;g;g--) putchar(b[g]+48);
}

inline bool cmp(vv a,vv b){return a.edge<b.edge;}

inline void add(int x,int y)
{
    cnt+=1;
    ver[cnt]=y; nex[cnt]=head[x]; head[x]=cnt;
}

inline int ff(int x)
{
    if(father[x]==x) return x;
    father[x]=ff(father[x]);
    return father[x];
}

inline void dfs1(int now,int fa)
{
    d[now]=d[fa]+1;	f[now]=fa; s[now]=1;
    for(RI i=head[now];i;i=nex[i])
    {
        int t=ver[i];
        dfs1(t,now);
        if(s[t]>s[wson[now]]) wson[now]=t;
        s[now]+=s[t];
    }
}

inline void dfs2(int now,int topp)
{
    top[now]=topp;
    if(wson[now]) dfs2(wson[now],topp);
    for(RI i=head[now];i;i=nex[i])
    {
        int t=ver[i];
        if(!top[t]) dfs2(t,t);
    }
}

inline int lca(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(d[top[x]]<d[top[y]])
        {
            int z=x;
            x=y; y=z;
        }
        x=f[top[x]];
    }
    return (d[x]>d[y]?y: x);
}

inline void kru()
{
    for(RI i=1;i<=m;i++)
    {
        int w=ff(v[i].fr), e=ff(v[i].ver);
        if(w!=e)
        {
            cn+=1;
            father[w]=father[e]=cn;
            add(cn,w);
            add(cn,e);
            edge[cn]=v[i].edge;
        }
    }
}

int main()
{
    n=gtt(); m=gtt(); cn=n;
    for(RI i=1;i<=4*n;i++) father[i]=i;
    for(RI i=1;i<=m;i++) {v[i].fr=gtt(); v[i].ver=gtt(); v[i].edge=gtt();}
    sort(v+1,v+1+m,cmp);
    kru();
    dfs1(cn,0);
    dfs2(cn,cn);
    n=gtt();
    for(RI i=1;i<=n;i++)
    {
        x=gtt(); y=gtt();
        if(ff(x)!=ff(y)) puts("impossible");
        else ptt(edge[lca(x,y)]), putchar('\n');
    }
}