USACO 6.5 Betsy's Tour （插头dp）

Betsy's Tour
Don Piele

A square township has been divided up into N² square plots (1 <= N <= 7). The Farm is located in the upper left plot and the Market is located in the lower left plot. Betsy takes her tour of the township going from Farm to Market by walking through every plot exactly once. Shown below is one possible tour for Betsy when N=3.

----------------
|    |    |    |
| F**********  |
|    |    | *  |
------------*---
|    |    | *  |
|  *****  | *  |
|  * | *  | *  |
---*---*----*---
|  * | *  | *  |
|  M | ******  |
|    |    |    |
----------------

Write a program that will count how many unique tours Betsy can take in going from Farm to Market for any value of N.

PROGRAM NAME: betsy

INPUT FORMAT

Line 1: A single integer N (1 <= N <= 7)

SAMPLE INPUT (file betsy.in)

3

OUTPUT FORMAT

A single line with a single integer, the number of unique tours.

SAMPLE OUTPUT (file betsy.out)

2

————————————————————题解

大意是从方块的左上角走到左下角，求一条哈密顿路

由于插头dp求哈密顿路需要一堆独立插头什么的，很麻烦，然后我们从起点到终点加一排，求哈密顿回路

然后我们发现我们再把这个图顺时针转90°它就会很舒服……

好啦，今天新学的一个算法……记录一下

求一个n*m图的哈密顿回路（哈密顿回路就是从一个点出发，图上的每一个点都经历一遍，再回到原点）

我们把一个格子向四周延伸记为插头

这样的话格子要么延伸，要么不延伸，如果延伸的话，它可以向四个方向延伸。

但是因为哈密顿回路嘛，我们如果有了一个延伸，肯定还要另一个延伸和它一起构成一个回路，很圆满，像这样。

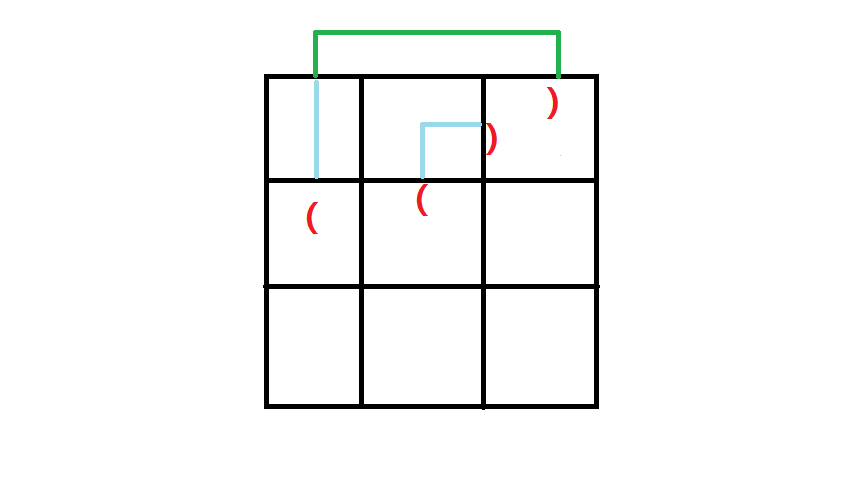
这里应用括号匹配的概念，我们用0表示没有延伸，1表示（ ， 2表示）

我们从上到下，从左到右枚举，对于一个新格子，我们需要知道它上方的格子的延伸情况，左方的格子延伸情况

当前格子设为（i，j）

如果上0，左0

那么当前格子必须两个方向都延伸

它对(i+1,j)的影响为1，对(i,j+1)的影响为2

ps：画的横线只是为了显示上左两个格子对第三个的影响，并不一定是用这条线段填充的格子

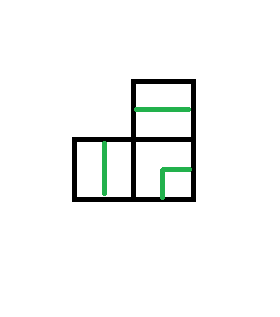
如果上0，左1

我们可以把左边的1过继过去

（对右面影响为1）

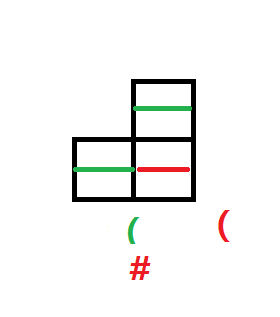
向下弯也一样（对下面影响为1）

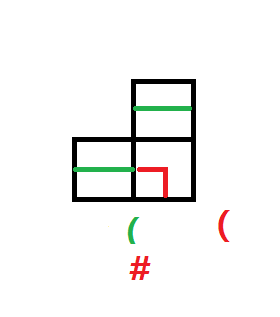
同理，如果上0左2，我们就把左边的2过继过去

如果上1或2，左0，我们把上面的1或2过继过去

如果上1，左1

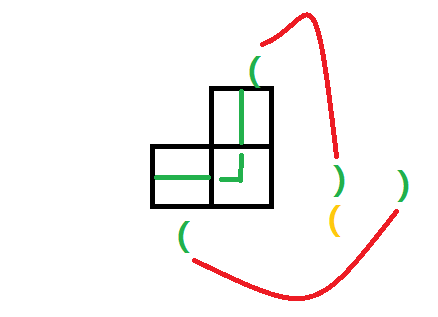
上左都有延伸当然是要把它们都连起来啦！然后找上方的1对应的2，将这个2更改成1（也就是橙色的括号更改）

上2左2和这是同理的，不过我们要找左边的2对应的1，将这个1更改成2

如果上1左2

简单地删掉就可以了

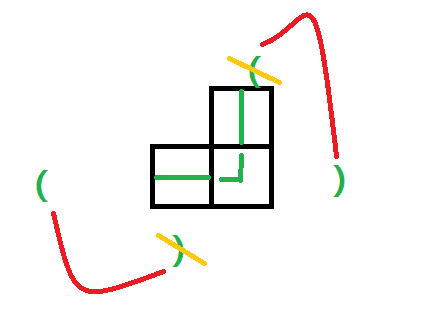
如果上2左1

恭喜你你找到答案了！因为这种情况只能出现在我们枚举到右下角填上哈密顿回路的最后一角！然后累加就可以了！

这道题就可以0.000过了

但是按照USACO的说法，这题就是个暴搜加优化，6章的剪枝真是多到吐……换换口味……

 /*
 LANG: C++
 PROG: betsy
 */
 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <cmath>
 #define siji(i,x,y) for(int i=(x) ; i <= (y) ; ++i)
 #define xiaosiji(i,x,y) for(int i = (x) ; i < (y); ++i)
 #define gongzi(j,x,y) for(int j = (x) ; j >= (y) ; --j)
 #define ivorysi
 #define mo 11447
 #define eps 1e-8
 #define o(x) ((x)*(x))
 using namespace std;
 typedef long long ll;
 /*
 0:#
 1:(
 2:)
 3:
 */
 int n,ans;
 int sum[][],hash[],code[][],base[],tot[];
 //用hash是因为可能会有不同的原始状态转移到同一个新状态
 //sum存储的是code[cur][i]情况数总和
 //code[cur][i]是四进制的压位后的编码
 void put_in_hash(int cur,int op,int data) {
     if(!hash[op]) {
         code[cur][++tot[cur]]=op;
         hash[op]=tot[cur];
     }
     sum[cur][hash[op]]+=data;
 }//这题很小，hash直接开就好，要不然还得挂link不断取模什么的
 int Change_state(int state,int pos,int val) {
     return state+val*(<<base[pos]);
 }
 int Get(int state,int pos) {
     return (state>>base[pos])&;
 }
 void solve() {
     scanf("%d",&n);
     if(n==) {puts("");return;}
     base[]=;
     siji(i,,) {
         base[i]=base[i-]+;
     }
     int cur=;
     code[][]=Change_state(code[][],,);
     code[][]=Change_state(code[][],n,);//把多添的一行的第一个设成1，第n个设成2，求回路
     sum[cur][]=,tot[cur]=;
     siji(i,,n) {
         siji(j,,n) {
             cur^=;//换情况
             tot[cur]=;
             memset(hash,,sizeof(hash));
             memset(sum[cur],,sizeof(sum[cur]));
             siji(k,,tot[cur^]) {
                 int state=code[cur^][k];
                 if(j==) state<<=;//移到1这一位相当于多了一个轮廓线
                 int p=Get(state,j+),q=Get(state,j);//p上方 q左方
                 state=Change_state(state,j+,-*p);state=Change_state(state,j,-*q);
                 //将拿出来的p、q删除
                 if(p== && q==) {
                     if(j!=n && i!=n) {
                         int change=Change_state(state,j,);//向下延伸
                         change=Change_state(change,j+,);//向右延伸
                         put_in_hash(cur,change,sum[cur^][k]);
                     }
                 }
                 if(p== && q>) {
                     if(j!=n){
                         int change=Change_state(state,j+,q);//向右延伸
                         put_in_hash(cur,change,sum[cur^][k]);
                     }
                     if(i!=n) {
                         int change=Change_state(state,j,q);//向下延伸
                         put_in_hash(cur,change,sum[cur^][k]);
                     }
                 }
                 if(p> && q==) {
                     if(j!=n) {
                         int change=Change_state(state,j+,p);//向右延伸
                         put_in_hash(cur,change,sum[cur^][k]);
                     }
                     if(i!=n) {
                         int change=Change_state(state,j,p);//向下延伸
                         put_in_hash(cur,change,sum[cur^][k]);
                     }
                 }
                 if(p== && q==) {
                     int change=state,l,top;
                     for(l = j+ ,top=;top;++l) {
                         if(Get(change,l)==) ++top;
                         if(Get(change,l)==) --top;
                     }
                     //不能直接找右侧第一个右括号，因为可能有这样((()))()()
                     //删掉前两个括号时，我们需要找第5个括号更改方向
                     change=Change_state(change,l-,-);//2-1=1
                     //2-1=1
                     //相当于把原值删除加上新值
                     put_in_hash(cur,change,sum[cur^][k]);
                 }
                 if(p== && q==) {
                     int change=state,l,top;
                     for(l = j- ,top=; top ;--l) {
                         if(Get(change,l)==) ++top;
                         if(Get(change,l)==) --top;
                     }
                     change=Change_state(change,l+,);//1+1=2
                     put_in_hash(cur,change,sum[cur^][k]);
                 }
                 if(p== && q==) {
                     int change=state;
                     put_in_hash(cur,change,sum[cur^][k]);
                 }
                 if(p==&&q==) {
                     if(i==n && j==n) ans+=sum[cur^][k];
                 }
             }
         }
     }
     printf("%d\n",ans);
 }
 int main(int argc, char const *argv[])
 {
 #ifdef ivorysi
     freopen("betsy.in","r",stdin);
     freopen("betsy.out","w",stdout);
 #else
     freopen("f1.in","r",stdin);
     //freopen("f1.out","w",stdout);
 #endif
     solve();
     return ;
 }

今天中考刚刚报完志愿，结果我又来敲了一天代码……我到底中考想考啥样……