【10.7校内测试】【队列滑窗】【2-sat】【贪心+栈二分+线段树（noip模拟好题）】【生日祭！】

比较好想的一道题，直接用队列滑窗，因为扫一遍往队列里加东西时，改变的只有一个值，开桶储存好就行了！

#include<bits/stdc++.h>
using namespace std;

int n, k, r;

inline int min(int a, int b) {
    return a > b ? b : a;
}

inline int max(int a, int b) {
    return a > b ? a : b;
}

int sum[], q[], cnt[], vis[], ned[];
int a[];

int main() {
    freopen("drop.in", "r", stdin);
    freopen("drop.out", "w", stdout);
    int T;
    scanf("%d", &T);
    while(T --) {
        memset(sum, , sizeof(sum));
        memset(q, , sizeof(q));
        memset(cnt, , sizeof(cnt));
        memset(vis, , sizeof(vis));
        memset(ned, , sizeof(ned));
        scanf("%d%d%d", &n, &k, &r);
        int tot = , fl = ;
        for(int i = ; i <= n; i ++) {
            scanf("%d", &a[i]);
            sum[a[i]] ++;
        }
        for(int i = ; i <= r; i ++) {
            int b, p;
            scanf("%d%d", &b, &p);
            if(!vis[b])    vis[b] = , tot ++;
            if(sum[b] < p) {
                fl = ; break;
            }
            ned[b] = max(ned[b], p);
        }
        if(fl) {
            printf("DESTROY ALL\n"); continue;
        }
        int ans = 0x3f3f3f3f;
        int h = , t = , now = ;
        for(int i = ; i <= n; i ++) {
            if(vis[a[i]]) {
                q[++t] = i; cnt[a[i]] ++; if(cnt[a[i]] == ned[a[i]]) now ++;
            }
            while(now == tot && h < t) {
                ans = min(ans, q[t] - q[h+] + );
                cnt[a[q[h+]]] --;
                if(cnt[a[q[h+]]] < ned[a[q[h+]]])    now --;
                h ++;
            }
        }
        printf("%d\n", ans);
    }
    return ;
} 

考场上想到$2-sat$但是忘得差不多了，打死都理不清楚关系。

这道题算是$2-sat$板子题了，主要是如何判断的思想。

首先题目条件疯狂暗示，但是和$2-sat$的一般理解方式不同。题目上给的约束条件我们按$2-sat$让他们避免相连，实际上就是题目中的防守文明，我们要摧毁文明，实际上是要让防守文明失效。即至少有一个点和它的负点相互相通。因为$n$很小就可以用两次$dfs$实现，然后就是分类讨论来判断该加几条边。

1、假如初始连边中就有某一个点对正负点相互连接，答案就是0.

2、假如一个点对中正点连向负点：

　  1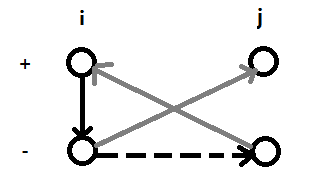）如果负点可以连向另一点对的正点，根据$2-sat$的对称行，另一点对的负点一定可以连向当前点对的正点，所以我们只用加条件$(i,j)$，就是在$-i$和$-j$之间连了一条边，使i点对相互连通。

　  2）如果负点没有连向任意点对的正点，那么一定无解，输出$No Way$。

3、假如一个点对中负点连向正点：

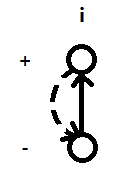那么只用加一个条件$(i,i)$，相当于在$i$和$-i$间连边即可。

4、假如点对之间没有连边：

1）将2、3结合，但是必须满足2的条件，这样加两条边即可。

2）没有2的条件，就无法加边，输出$No Way$。

#include<bits/stdc++.h>
using namespace std;

struct Node {
    int u, v, nex;
    Node(int u = , int v = , int nex = ) :
        u(u), v(v), nex(nex) { }
} Edge[];

int h[], stot;
void add(int u, int v) {
    Edge[++stot] = Node(u, v, h[u]);
    h[u] = stot;
}

int vis[];
void dfs(int u) {
    vis[u] = ;
    for(int i = h[u]; i; i = Edge[i].nex) {
        int v = Edge[i].v;
        if(vis[v])    continue;
        dfs(v);
    }
}

int n, m;
int main() {
    freopen("god.in", "r", stdin);
    freopen("god.out", "w", stdout);
    int T;
    scanf("%d", &T);
    while(T --) {
        memset(h, , sizeof(h));
        stot = ;
        scanf("%d%d", &n, &m);
        for(int i = ; i <= m ; i++) {
            int x, y;
            scanf("%d%d", &x, &y);
            if(x >  || y < ) swap(x, y);
            if(x >  && y > ) {
                add(x, y + n);
                add(y, x + n);
            }
            if(x <  && y < ) {
                add(-x + n, -y);
                add(-y + n, -x);
            }
            if(x <  && y > ) {
                add(-x + n, y + n);
                add(y, -x);
            }
        }
        int tag1 = , tag2 = , tag0 = ;
        for(int i = ; i <= n; i ++) {
            memset(vis, , sizeof(vis));
            dfs(i);
            int fl = ;
            if(vis[i + n]) {
                memset(vis, , sizeof(vis));
                dfs(i + n);
                fl = ;
                if(vis[i]) {
                    tag0 = ; break;
                }
                for(int j = ; j <= n; j ++) {
                    if(j != i && vis[j]) {
                        tag1 = ; break;
                    }
                }
            }
            memset(vis, , sizeof(vis));
            dfs(i + n);
            if(vis[i]) {
                tag1 = ;
            } else if(!fl) {
                for(int j = ; j <= n; j ++) {
                    if(j != i && vis[j]) {
                        tag2 = ; break;
                    }
                }
            }
        }
        if(tag0)        printf("0\n");
        else if(tag1)    printf("1\n");
        else if(tag2)    printf("2\n");
        else            printf("No Way\n");
    }

    return ;
}

一道好题。（但是现在不想写题解了aaaa）

所以复制题解~

60分：

考虑这样一个贪心：
先从左往右扫，如果某一时刻不满足要求，则需要删除前面中某一个支持对方的人。我们贪心地选择删除当前时刻访问的人（肯定是支持对方），然后继续往后扫。
然后再从右往左扫，作相同的操作。
直观地理解是这样的：我们尽量删除靠右的人，使得从右往左扫时少删除一些人。
可以采用交换论证法证明这贪心是对的。

80-100：

首先我们可以发现从左往右扫完，从右往左扫的这个过程可以不用实现出来。只需要求出右端点开始的最小后缀和的相反数即可。
然后我们发现，如果两个询问区间拥有相同的左端点，则只需要作一次从左往右扫的工作。这使我们想到要离线化解决问题。

我们将询问按左端点排序，按照左端点从大到小的顺序求解询问。
如果已知从 i 开始向右扫需要删除那些结点，则从 i-1 开始向右扫需要删除那些结点可以快速求出。具体来说，如果i-1是支持者，则左数第一个被删除的结点与它抵消；如果i-1是反对者，则加入被删除的结点里。
该过程可以用栈维护。

通过在栈里面二分，我们可以知道区间[l, r]在从左往右扫时需要删除的结点数量。
现在问题就是求解以 r 为端点的最小后缀和。
这个东西可以用块状数组O(sqrt(N))维护（这就是80%算法的由来），更好的方法应该是用线段树O(log(N))维护
于是该题就在O((N+Q)logN)的时间复杂度内解决了。

#include<bits/stdc++.h>
using namespace std;

struct Tree {
    int mi, sum;
} TR[*];

int n, m;
char s[];

void update(int nd) {
    TR[nd].mi = min(TR[nd <<  | ].mi, TR[nd << ].mi + TR[nd <<  | ].sum);
    TR[nd].sum = TR[nd << ].sum + TR[nd <<  | ].sum;
}

void build(int nd, int l, int r) {
    if(l == r) {
        TR[nd].mi = TR[nd].sum = ;
        return ;
    }
    int mid = (l + r) >> ;
    build(nd << , l, mid);
    build(nd << , mid + , r);
    update(nd);
}

void modify(int nd, int l, int r, int pos, int d) {
    if(l == r) {
        TR[nd].sum = d;
        TR[nd].mi = d;
        return ;
    }
    int mid = (l + r) >> ;
    if(pos <= mid)    modify(nd << , l, mid, pos, d);
    else            modify(nd <<  | , mid + , r, pos, d);
    update(nd);
}

Tree query(int nd, int l, int r, int pos) {
    if(l == r) return TR[nd];
    int mid = (l + r) >> ;
    if(pos <= mid)    return query(nd << , l, mid, pos);
    else {
        Tree res = query(nd <<  | , mid + , r, pos);
        res.mi = min(res.mi, res.sum + TR[nd << ].mi);
        res.sum = res.sum + TR[nd << ].sum;
        return res;
    }
}

vector < pair < int , int > > qus[];
int tp = , stk[], ans[];

int find(int pos) {
    int l = , r = tp, an = tp + ;
    while(l <= r) {
        int mid = (l + r) >> ;
        if(stk[mid] > pos)    l = mid + ;
        else an = mid, r = mid - ;
    }
    return an;
}

int main() {
    freopen("sworder.in", "r", stdin);
    freopen("sworder.out", "w", stdout);
    scanf("%d", &n);
    scanf("%s", s + );
    scanf("%d", &m);
    for(int i = ; i <= m; i ++) {
        int l, r;
        scanf("%d%d", &l, &r);
        qus[l].push_back(make_pair(r, i));
    }
    build(, , n);
    for(int i = n; i >= ; i --) {
        if(s[i] == 'C')    stk[++tp] = i;
        else {
            if(tp) {
                modify(, , n, stk[tp], -);
                stk[tp--] = ;
            }
            modify(, , n, i, );
        }
        for(int j = ; j < qus[i].size(); j ++) {
            int pos = qus[i][j].first;
            int tmp = find(pos);
            ans[qus[i][j].second] = (tp - tmp + ) - min(, query(, , n, pos).mi);
        }
    }
    for(int i = ; i <= m; i ++)    printf("%d\n", ans[i]);
    return ;
}