【CodeForces】961 G. Partitions 斯特林数

【题目】G. Partitions

【题意】n个数$w_i$，每个非空子集S的价值是$W(S)=|S|\sum_{i\in S}w_i$，一种划分方案的价值是所有非空子集的价值和，求所有划分成k个非空子集的方案的价值和。1<=k<=n<=2*10^5，1<=wi<=10^9。

【算法】斯特林数

【题解】首先价值与具体数字没有关系，即：

$$ans=num*\sum_{i=1}^{n}w_i$$

其中num表示1在每个k划分方案中所在集合的大小的和。

考虑一种角度，所在集合的大小可以视为所在集合的每个数字贡献了1的价值，那么答案就是1和每个数字在同一个集合的方案数，即：

$$num=\begin{Bmatrix}n\\ k\end{Bmatrix}+(n-1)*\begin{Bmatrix}n-1\\ k\end{Bmatrix}$$

其中1自己的贡献是s(n,k)，其余n-1个数字的贡献是将它和1视为整体的方案数s(n-1,k)。

斯特林数可以用通项公式O(k)计算，总复杂度O(n ln n)。

（代码略）

以上是正解，但一般人很容易yy出下面的等式：

$$num=\sum_{i=1}^{n}i*\binom{n-1}{i-1}\begin{Bmatrix}n-i\\ k-1\end{Bmatrix}$$

即枚举1所在集合大小。

两式必然等价，证明如下：

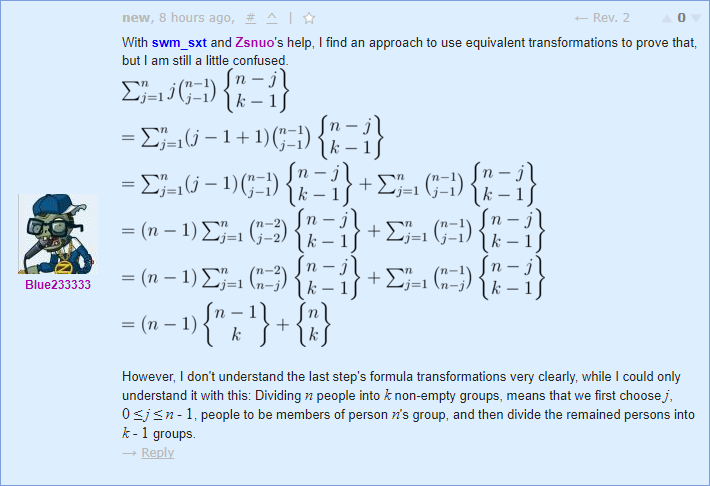
最后一步是通过实际含义，即枚举j，n-2个人中选n-j个人，这n-j个人分成k-1组的方案，相当于枚举n-1个人中第一个人所在集合的大小，所以等价于s(n-1,k)。

另一种写法：【CF961G】Partitions 第二类斯特林数

非常经典的，把斯特林数暴力拆分然后往前提，快速处理后面的组合数

把组合数通过分解i变成C(n-1,i-1)的形式，然后可以用二项式定理化简。