Task 4.4二维环形数组求最大子矩阵之和

任务：

（1）输入一个二维整形数组，数组里有正数也有负数。

（2）二维数组首尾相接，象个一条首尾相接带子一样。

（3）数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

（4）求所有子数组的和的最大值。

1.设计思想：这个题目显然是结合了之前二维数组求最大子数组的和以及一维环形数组求最大连续子数组的和两个模块，所以只要将两个程序联合起来即可。首先将数组横向扩展一倍，将环转换为求一维连续的数组求最大子数组和。然后将二维数组转换为一维数组求和，即建立一个新的和数组，用来储存从数组的首个元素到当前位置元素的连续子数组的最大和，其中会用到一位数组求连续最大子数组程序中的部分代码。然后这个问题就可以被转化为求新的和数组中的最大元素了，就能很方便地求出最大子矩阵的和。

2.源代码：

//二维环形数组求最大子矩阵
//刘子晗 2015/4/22

#include<iostream>
#include<time.h>
using namespace std;

void main()
{
    int m, n, a[][], b[][],i, j ;
    cout << "请输入矩阵的行数和列数：" << endl;
    cin >> m >> n;
    srand((unsigned)time(NULL));
    cout << "产生的随机数组为：" << endl;

for (i = ; i < m; i++)
    {
        for (j = ; j < n; j++)
        {
            a[i][j] = rand() %  - ;
            cout << a[i][j] << " ";
        }
        cout << endl;
    }//输出随机产生的矩阵

    int max = a[][];
    for (i = ; i < m ; i++)
    {
        for (j = ; j < n; j++)
        {
            a[i][j + n] = a[i][j];
        }
    }//对二维数组进行扩展，横向延长一倍

    cout << "扩展后环形数组为：" << endl;
    for (i = ; i < m; i++)
    {
        for (j = ; j < *n-; j++)
        {
            cout << a[i][j] << ' ';
        }
        cout << endl;
    }//输出扩展之后的新数组

    for (i = ; i < ; i++)
    {
        b[][] = a[][];
        for (j = ; j <  *n -; j++)
        {
            if (a[][j - ] < )
            {
                b[][j] = a[][j];
            }
            else
            {
                b[][j] = b[][j - ] + a[][j];
            }
        }
    }//对第一行的数作为一个数组求其最大连续子数组之和

    for (i = ; i < m; i++)
    {
        for (j = ; j < ; j++)
        {
            if (a[i - ][] < )
            {
                b[i][] = a[i][];
            }
            else
            {
                b[i][] = b[i - ][] + a[i][];
            }
        }
    }//对第一列的数作为一个数组，求其连续子数组的最大和

    for (i = ; i<m; i++)
    {
        for (j = ; j<*n-; j++)
        {
            if (b[i - ][j - ]<)
            {
                if (b[i - ][j] >=  && b[i][j - ] >= )
                {
                    if (b[i][j - ] >= b[i - ][j])
                    {
                        b[i][j] = b[i][j - ] + a[i][j];
                    }
                    else
                    {
                        b[i][j] = b[i - ][j] + a[i][j];
                    }
                }
                else if (b[i - ][j] >=  && b[i][j - ] <= )
                {
                    b[i][j] = b[i - ][j] + a[i][j];
                }
                else if (b[i - ][j] <=  && b[i][j - ] >= )
                {
                    b[i][j] = b[i][j - ] + a[i][j];
                }
                else
                {
                    b[i][j] = a[i][j];
                }
            }
            else
            {
                if (b[i - ][j] >=  && b[i][j - ] >= )
                {
                    b[i][j] = a[i][j] + b[i - ][j] + b[i][j - ] - b[i - ][j - ];
                }
                else if (b[i - ][j] >=  && b[i][j - ] <= )
                {
                    b[i][j] = a[i][j] + b[i - ][j] - b[i - ][j - ];
                }
                else if (b[i - ][j] <=  && b[i][j - ] >= )
                {
                    b[i][j] = a[i][j] + b[i][j - ] - b[i - ][j - ];
                }
                else
                {
                    b[i][j] = a[i][j];
                }
            }
        }
    }//求整个矩阵中从首个元素到当前元素的数组和的最大值，并将该值赋给当前地址

    cout << "子矩阵的和数组为：" << endl;
    for (i = ; i<m; i++)
    {
        for (j = ; j< * n - ; j++)
        {
            cout << b[i][j] << " ";
        }
        cout << endl;
    }//输出新生成的和数组

    cout << endl;
    for (i = ; i<m; i++)
    {
        for (j = ; j< * n - ; j++)
        {
            if (b[i][j]>max)
            {
                max = b[i][j];
            }

        }
    }//求数组中的最大元素
    cout << "最大子矩阵和为：" << max << endl;
}

3.结果截图：

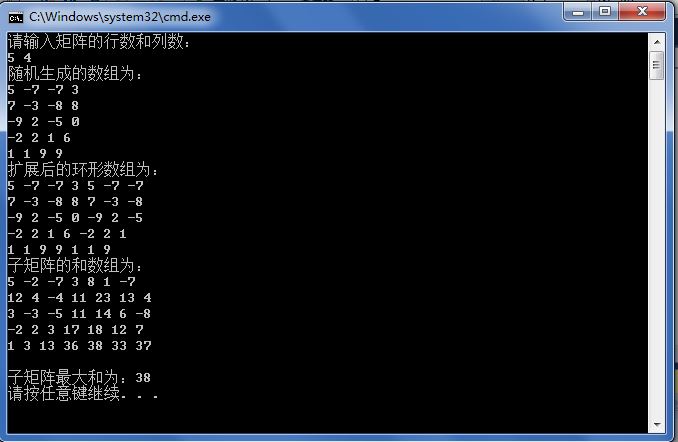
4.总结：（1）再一次感觉到拆分问题的重要性，无论题目有多复杂，当拥有可以拆分问题的能力的时候，一一击破然后再将其有机地组合起来，一切问题都会迎刃而解；

（2）题目在一步一步地增加难度的时候，如果能把之前的每个相对简单的程序都弄明白之后，组合成的难题反而却是非常简单的。所以每次完成一个程序一定要完全把它想清楚，非以方便以后去使用其中的内容和思想；

（3）要善于总结，每一次总结回顾总能发现不一样的问题，得到不一样的体会。