NOIP2016 天天爱跑步 80分暴力

https://www.luogu.org/problem/show?pid=1600

题目描述

小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。«天天爱跑步»是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

这个游戏的地图可以看作一一棵包含 个结点和 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从到的连续正整数。

现在有个玩家,第个玩家的起点为 ,终点为  。每天打卡任务开始时,所有玩家在第秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点的观察员会选择在第秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第秒也理到达了结点  。 小C想知道每个观察员会观察到多少人?

注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点作为终点的玩家: 若他在第秒重到达终点,则在结点的观察员不能观察到该玩家;若他正好在第秒到达终点,则在结点的观察员可以观察到这个玩家。

输入输出格式

输入格式：

第一行有两个整数和 。其中代表树的结点数量, 同时也是观察员的数量, 代表玩家的数量。

接下来 行每行两个整数和 ,表示结点 到结点 有一条边。

接下来一行 个整数,其中第个整数为 , 表示结点出现观察员的时间。

接下来 行,每行两个整数,和,表示一个玩家的起点和终点。

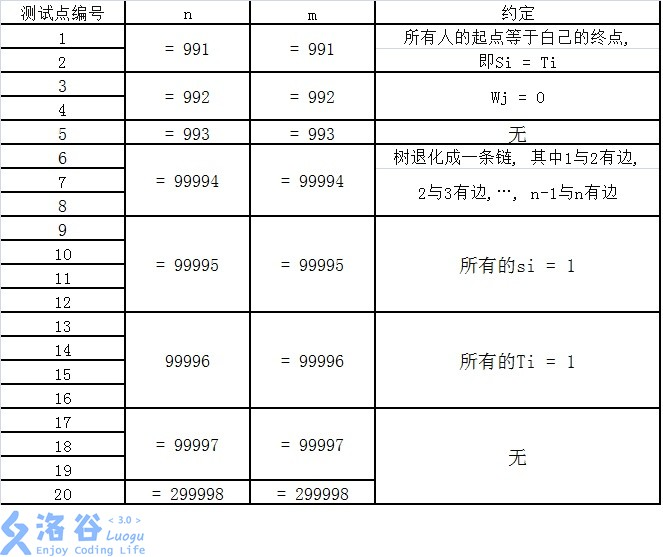
对于所有的数据,保证 。

输出格式：

输出1行 个整数,第个整数表示结点的观察员可以观察到多少人。

输入输出样例

输入样例#1：

6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6 

输出样例#1：

2 0 0 1 1 1 

输入样例#2：

5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5 

输出样例#2：

1 2 1 0 1 

正解移步 http://www.cnblogs.com/TheRoadToTheGold/p/6677435.html

测试点1——5：

数组a[i][j]表示点i在j时刻经过的人数，然后一个人一个人的dfs，记录时刻time

如果到了终点，递归回退时a[now][time]++

令watch[i]=j表示i号节点观察员在j时刻出现

输出a[i][watch[i]]

void run(int now,int end,int time,int fa)
{
    if(now==end)
    {
        ok=true;
        a[now][time]++;
        return;
    }
    if(ok) return;
    for(int i=front[now];i;i=nextt[i])
    {
        if(to[i]==fa) continue;
        run(to[i],end,time+,now);
    }
    if(ok) a[now][time]++;
}

测试点6——8：

树退化为一条链，而且点的编号就是深度

所以对于链上一个观察员，他只能观察到从两个位置出发的人i+watch[i]，i-watch[i]

如果i能观察到起点深度比他小的人，那么这个人的终点要>=i

如果i能观察到起点深度比他大的人，那么这个人的终点要<=i

所以，

用链表存储从每个节点起跑的人，

枚举每个观察员，然后判断两个位置的人是否满足要求

void solve2()
{
    for(int i=;i<=n;i++)
    {
        if(i-watch[i]>=)
        {
            for(int j=front[i-watch[i]];j;j=nextt[j])
            {
                if(i<=e[to[j]].t)  ans[i]++;
            }
        }
        if(i+watch[i]<=n)
        {
            for(int j=front[i+watch[i]];j;j=nextt[j])
            {
                if(i>=e[to[j]].t) ans[i]++;
            }
        }
    }
}

测试点9——12：

所有人的起点都是1，假设1号的深度为0，

那么只有观察员节点的深度等于出现时间，他才能观察到

所以先判断深度是否等于出现时间，不等，直接输出0，下一个

若相等，他一定能观察到经过他的所有人

也就是说，以观察员i为根的子树中有跑步者的终点，观察员i就能观察多少人

所以，终点+1，记录每个节点的深度，我用的bfs，单后dfs统计子树1的个数，

kids[]表示答案

void bfs1()
{
    queue<node2>q;
    cur.d= ;cur.who=; fa[]=;
    q.push(cur);
    while(!q.empty())
    {
        cur=q.front(); q.pop();
        for(int i=front[cur.who];i;i=nextt[i])
        {
            if(to[i]==fa[cur.who]) continue;
            fa[to[i]]=cur.who;
            nxt.d=cur.d+; nxt.who=to[i]; deep[nxt.who]=deep[cur.who]+;
            q.push(nxt);
        }
    }
}
void dfs1(int now)
{
    kids[now]=sum[now];
    for(int i=front[now];i;i=nextt[i])
    {
        if(to[i]==fa[now]) continue;
        dfs1(to[i]);
        kids[now]+=kids[to[i]];
    }
}

测试点13——16：

所有人的终点都是1

也就是说，第i个观察员只能观察到第deep[i]+watch[i]层的跑步者

所以，若跑步者能被观察员i观察到，要满足以下两个条件：

1、在起点观察员i的子树内

2、起点的层数=deep[i]+watch[i]

先对原树dfs一遍，记录观察员i的子树dfs序范围in[i]——out[i]

对每一层维护一颗线段树，动态开节点

查询时，找到deep[i]+watch[i]这一层的线段树，查in[i]——out[i]有多少个起点

void add(int &now,int pos,int l,int r,int cnt)
{
    if(!now) now=++tot2;
    sum[now]+=cnt;
    if(l==r) return;
    int mid=l+r>>;
    if(pos<=mid) add(lc[now],pos,l,mid,cnt);
    else add(rc[now],pos,mid+,r,cnt);
}
void dfs(int now,int pre)
{
    in[now]=++tot;
    add(root[deep[now]],tot,,n,siz[now]);
    for(int i=front[now];i;i=nxt[i])
    {
        if(to[i]==pre) continue;
        deep[to[i]]=deep[now]+;
        maxn=max(maxn,deep[to[i]]);
        dfs(to[i],now);
    }
    out[now]=tot;
}
void query(int now,int opl,int opr,int l,int r)
{
    if(!now) return;
    if(l>=opl&&r<=opr) { ans+=sum[now]; return; }
    int mid=l+r>>;
    if(opl<=mid) query(lc[now],opl,opr,l,mid);
    if(opr>mid) query(rc[now],opl,opr,mid+,r);
}

测试点17——20：

正解移步 http://www.cnblogs.com/TheRoadToTheGold/p/6677435.html

所有暴力综合代码

#include<queue>
#include<cstdio>
#include<algorithm>
#define N1 1000
#define N2 100000
#define N3 300000
using namespace std;
int n,m,uu,vv;
int watch[N2];
int front[N2],nextt[N2*],to[N2*],tot;
void add(int u,int v)
{
    to[++tot]=v; nextt[tot]=front[u]; front[u]=tot;
}
namespace one_to_five
{
    int a[N1][N1];
    bool ok;
    void run(int now,int end,int time,int fa)
    {
        if(now==end)
        {
            ok=true;
            a[now][time]++;
            return;
        }
        if(ok) return;
        for(int i=front[now];i;i=nextt[i])
        {
            if(to[i]==fa) continue;
            run(to[i],end,time+,now);
        }
        if(ok) a[now][time]++;
    }
    void solve()
    {
        for(int i=;i<n;i++)
        {
            scanf("%d%d",&uu,&vv);
            add(uu,vv);
            add(vv,uu);
        }
        for(int i=;i<=n;i++) scanf("%d",&watch[i]);
        for(int i=;i<=m;i++)
        {
            scanf("%d%d",&uu,&vv);
            ok=false;
            run(uu,vv,,);
        }
        for(int i=;i<=n;i++) printf("%d ",a[i][watch[i]]);
    }
}
namespace six_to_eight
{
    struct node { int s,t; } e[N2];
    int ans[N2];
    void solve2()
    {
        for(int i=;i<=n;i++)
        {
            if(i-watch[i]>=)
            {
                for(int j=front[i-watch[i]];j;j=nextt[j])
                {
                    if(i<=e[to[j]].t)  ans[i]++;
                }
            }
            if(i+watch[i]<=n)
            {
                for(int j=front[i+watch[i]];j;j=nextt[j])
                {
                    if(i>=e[to[j]].t) ans[i]++;
                }
            }
        }
    }
    void solve()
    {
        for(int i=;i<n;i++) scanf("%d%d",&uu,&vv);
        for(int i=;i<=n;i++) scanf("%d",&watch[i]);
        for(int i=;i<=m;i++)
        {
            scanf("%d%d",&e[i].s,&e[i].t);
            add(e[i].s,i);
        }
        solve2();
        for(int i=;i<=n;i++) printf("%d ",ans[i]);
    }
}
namespace nine_to_twelve
{
    struct node2 { int d,who; }cur,nxt;
    int sum[N2],deep[N2],fa[N2],kids[N2];
    void bfs1()
    {
        queue<node2>q;
        cur.d= ;cur.who=; fa[]=;
        q.push(cur);
        while(!q.empty())
        {
            cur=q.front(); q.pop();
            for(int i=front[cur.who];i;i=nextt[i])
            {
                if(to[i]==fa[cur.who]) continue;
                fa[to[i]]=cur.who;
                nxt.d=cur.d+; nxt.who=to[i]; deep[nxt.who]=deep[cur.who]+;
                q.push(nxt);
            }
        }
    }
    void dfs1(int now)
    {
        kids[now]=sum[now];
        for(int i=front[now];i;i=nextt[i])
        {
            if(to[i]==fa[now]) continue;
            dfs1(to[i]);
            kids[now]+=kids[to[i]];
        }
    }
    void solve()
    {
        int u,v;
        for(int i=;i<n;i++)
        {
            scanf("%d%d",&uu,&vv);
            add(uu,vv);
            add(vv,uu);
        }
        bfs1();
        for(int i=;i<=n;i++) scanf("%d",&watch[i]);
        for(int i=;i<=m;i++)
        {
            scanf("%d%d",&uu,&vv);
            sum[vv]++;
        }
        dfs1();
        for(int i=;i<=n;i++)
         if(watch[i]==deep[i]) printf("%d ",kids[i]);
         else printf("0 ");
    }
}
namespace thirteen_to_sixteen
{
    int ans,tot2,maxn;
    int watch[N2],siz[N2];
    int in[N2],out[N2],deep[N2];
    int root[N2],lc[N2*],rc[N2*],sum[N2*];
    void insert(int &now,int pos,int l,int r,int cnt)
    {
        if(!now) now=++tot2;
        sum[now]+=cnt;
        if(l==r) return;
        int mid=l+r>>;
        if(pos<=mid) insert(lc[now],pos,l,mid,cnt);
        else insert(rc[now],pos,mid+,r,cnt);
    }
    void dfs(int now,int pre)
    {
        in[now]=++tot;
        insert(root[deep[now]],tot,,n,siz[now]);
        for(int i=front[now];i;i=nextt[i])
        {
            if(to[i]==pre) continue;
            deep[to[i]]=deep[now]+;
            maxn=max(maxn,deep[to[i]]);
            dfs(to[i],now);
        }
        out[now]=tot;
    }
    void query(int now,int opl,int opr,int l,int r)
    {
        if(!now) return;
        if(l>=opl&&r<=opr) { ans+=sum[now]; return; }
        int mid=l+r>>;
        if(opl<=mid) query(lc[now],opl,opr,l,mid);
        if(opr>mid) query(rc[now],opl,opr,mid+,r);
    }
    void solve()
    {
        for(int i=;i<n;i++)
        {
            scanf("%d%d",&uu,&vv);
            add(uu,vv);
        }
        for(int i=;i<=n;i++)  scanf("%d",&watch[i]);
        tot=;
        while(m--)
        {
            scanf("%d%d",&uu,&vv);
            siz[uu]++;
        }
        dfs(,);
        for(int i=;i<=n;i++)
        {
            ans=;
            if(deep[i]+watch[i]<=maxn) query(root[deep[i]+watch[i]],in[i],out[i],,n);
            printf("%d ",ans);
        }
    }

}
int main()
{
    scanf("%d%d",&n,&m);
    if(n%<=) one_to_five::solve();
    else if(n%==) six_to_eight::solve();
    else if(n%==) nine_to_twelve::solve();
    else if(n%==) thirteen_to_sixteen::solve();
}