UVA 5009 Error Curves

Problem Description

Josephina is a clever girl and addicted to Machine Learning recently. She
pays much attention to a method called Linear Discriminant Analysis, which
has many interesting properties.
In order to test the algorithm's efficiency, she collects many datasets.
What's more, each data is divided into two parts: training data and test
data. She gets the parameters of the model on training data and test the
model on test data. To her surprise, she finds each dataset's test error
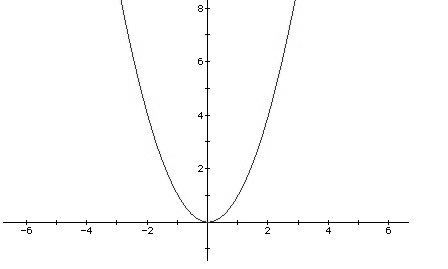
curve is just a parabolic curve. A parabolic curve corresponds to a
quadratic function. In mathematics, a quadratic function is a polynomial
function of the form f(x) = ax2 + bx + c. The
quadratic will degrade to linear function if a = 0.

It's very easy to calculate the minimal error if there is only one test
error curve. However, there are several datasets, which means Josephina
will obtain many parabolic curves. Josephina wants to get the tuned
parameters that make the best performance on
all datasets. So she should take all error curves into account, i.e.,
she has to deal with many quadric functions and make a new error
definition to represent the total error. Now, she focuses on the
following new function's minimum which related to multiple
quadric functions. The new function F(x) is defined as follows: F(x) =
max(Si(x)), i = 1...n. The domain of x is [0, 1000]. Si(x) is a quadric
function. Josephina wonders the minimum of F(x). Unfortunately, it's too
hard for her to solve this problem. As a
super programmer, can you help her?

Input

The input contains multiple test cases. The first line is the number of
cases T (T < 100). Each case begins with a number n (n ≤ 10000).
Following n lines, each line contains three integers a (0 ≤ a ≤ 100), b
(|b| ≤ 5000), c (|c| ≤ 5000), which mean the corresponding
coefficients of a quadratic function.

Output

For each test case, output the answer in a line. Round to 4 digits after the decimal point.

Sample Input

2

1

2 0 0

2

2 0 0

2 -4 2

Sample Output

0.0000

0.5000

画图理解一下，

几个下凸函数取max仍然是下凸函数

然后三分就行了

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 double eps=1e-;
 double a[],b[],c[];
 int n;
 double cal(double x)
 {int i;
   double tmp=a[]*x*x+b[]*x+c[];
   for (i=;i<=n;i++)
     {
       tmp=max(tmp,a[i]*x*x+b[i]*x+c[i]);
     }
   return tmp;
 }
 int main()
 {int T,i;
   cin>>T;
   while (T--)
     {
       cin>>n;
       for (i=;i<=n;i++)
     {
       scanf("%lf%lf%lf",&a[i],&b[i],&c[i]);
     }
       int t=;
       double l=,r=,ans=;
       while (t--)
     {
       double mid1=l+(r-l)/3.0,mid2=r-(r-l)/3.0;
       if (cal(mid1)<cal(mid2)) r=mid2;
       else l=mid1;
     }
       printf("%.4lf\n",cal(l));
     }
 }