Fast R-CNN中的边框回归

前面对R-CNN系的目标检测方法进行了个总结，其中对目标的定位使用了边框回归，当时对这部分内容不是很理解，这里单独学习下。

R-CNN中最后的边框回归层，以候选区域(Region proposal)为输入，来对Region proposal中包含的目标进行准将的定位。但是，这个输入的候选区域通常不会正确的包含目标区域，如下图：

绿色边框是飞机的Ground Truth边框，绿色的是Region proposal边框，虽然Region proposal中包含了目标飞机，但是其定位却不是很准确，这就需要对候选区域的边框进行修正，调整其位置和大小，以使其能够更为接近绿色的Ground Truth边框。

边框回归的方法

无论是Ground Truth边框还是Region proposal边框，可以使用一个四元组\((x,y,w,h)\)来表示。其中，\((x,y)\)表示边框的中心位置，\((w,h)\)表示边框的宽和高。
在边框回归时，实际就是找到一种变换，使修正的后的Region proposal边框位置和Ground Truth边框尽可能的接近，公式表示如下：
\[
f(P_x,P_y,P_w,P_h) \approx (G_x,G_y,G_w,G_h)
\]
其中，\((P_x,P_y,P_w,P_h)\)输入的候选区域的边框,\((G_x,G_y,G_w,G_h)\)是Ground Truth边框。

那么这种变换\(f\)怎么进行呢？

观察边框的四元组表示\((x,y)\)表示中心位置，对于位置的修正通常使用平移；\((w,h)\)表示边框的宽和高，则可以使用缩放进行修正。也就是对边框的回归修正，

对边框的中心位置进行平移\((\Delta x,\Delta y)\)
\[
\begin{align*}
\Delta x &= P_w d_x(P) \\
\Delta y &= P_h d_y(P)
\end{align*}
\]
则修正的中心位置就是
\[
\begin{align*}
\hat{G_x} &= P_w d_x(P) + P_x \\
\hat{G_y} &= P_h d_y(P) + P_y
\end{align*}
\]
对边框的宽和高进行缩放\((S_w,S_h)\),
\[
\begin{align*}
S_w &= exp(d_w(P)) \\
S_h &= exp(d_h(P))
\end{align*}
\]
修正后的边框的宽和高为
\[
\begin{align*}
\hat{G_w} &= P_w exp(d_w(P)) \\
\hat{G_h} &= P_h exp(d_h(P))
\end{align*}
\]

修正后的边框\((\hat{G_x},\hat{G_y},\hat{G_w},\hat{G_h} )\)要近似等于Ground Truth的边框。

通过上述公式可以知道，边框回归实际上就是学习\(d_x(P),d_y(P),d_w(P),d_h(P)\)这4个变换。在边框回归的全连接层，输入的是候选区域的特征信息\(X\)以及其边框信息\(P\)，要学习的是全连接层的权值矩阵\(W\)，也就说回归的全连接层就实现了上述变换，输出的是\(d_x(P),d_y(P),d_w(P),d_h(P)\)，经过上述公式的可以得到平移和缩放\((\Delta x,\Delta y,S_w,S_h)\)。对候选区域的边框进行该平移和缩放得到的边框尽可能的和Ground Truth相近。

学习得到的\(d_x(P),d_y(P),d_w(P),d_h(P)\)通过数码的公式可以很容易得到\((\Delta x,\Delta y,S_w,S_h)\)，也可以说学习得到的是\((\Delta x,\Delta y,S_w,S_h)\)。这两者没有区别，不用做区分。但是在计算预测边框位置的时候，需要注意。

损失函数

R-CNN使用一个全连接网络实现边框的回归，

其输入的是候选区域的特征及其边框\((P_x,P_y,P_w,P_h)\)
输出的该候选框要进行的平移和缩放\((\Delta x,\Delta y,S_w,S_h)\)。
要学习的是权值矩阵\(W\)，以使候选框进行\((\Delta x,\Delta y,S_w,S_h)\)变换后，尽可能和Ground Truth接近。

有了以上认识，来看下损失函数的设计
\[
L(p,u,t^u,v) = L_{cls}(p,u) + \lambda [u \ge 1]L_{Ioc}(t^u,v)
\]
其中，\(L_{cls}(p,u)\)是分类的损失函数，\(p_u\)是class u的真实分类的概率。这里，约定\(u = 0\)表示背景，不参与边框回归的损失计算。上面是Fast R-CNN将分类的损失和边框回归的损失放到了一起，这里这关注边框回归的损失
\[
\begin{align*}
L_{Ioc}(t^u,v) &= \sum_{i \in {x,y,w,h}}smooth_{L_1}(t_i^u - v)
\end{align*}
\]
其中，\(u\)表示类别，\(t^u\)表示预测边框的偏移量（也就是预测边框进行\(t^u\)偏移后，能够和真实边框最接近），\(v\)表示预测边框和实际边框之间真正的偏移量。
也就是\(t^u = (\Delta x,\Delta y,S_w,S_h)\)为学习得到的偏移量，而\(v\)则是输入的候选区域的边框和Ground Truth的真正偏移。

训练样本偏移\(v\)的构造

我们使用下面的公式描述了边框修正的过程
\[
\begin{align*}
\hat{G_x} &= \Delta x + P_x \\
\hat{G_y} &= \Delta y + P_y \\
\hat{G_w} &= P_w S_w ,S_w = exp(d_w(P))\\
\hat{G_h} &= P_h S_h,S_h = exp(d_h(P))
\end{align*}
\]
\(P\)为输入的边框，\(\hat{G}\)为修正后的边框，修正使用的平移和缩放为\((\Delta x,\Delta y,S_w,S_h)\)。通过上述的公司，就可以得到训练样本\(P = (P_x,P_y,P_w,P_h)\)相对于Ground Truth\(G = (G_x,G_y,G_w,G_h)\)边框的真实偏移量\(v\)
\[
\begin{align*}
v_x &= (G_x - P_x) / P_w \\
v_y &= (G_y - P_y) / P_h \\
v_w &= log(G_w / P_w) \\
v_h &=log(G_h / P_h)
\end{align*}
\]

偏移量的构造

边框回归的偏移量使如下公式表示
\[
\begin{align*}
\Delta x &= P_w d_x(P) \\
\Delta y &= P_h d_y(P) \\
S_w &= exp(d_w(P)) \\
S_h &= exp(d_h(P))
\end{align*}
\]

从上面公式可知，从边框回归的学习得到的\(d_x(P),d_y(P),d_w(P),d_h(P)\)并没有直接用于平移和缩放，而是加了一步处理：对于平移，添加了比例宽高比例因子；宽和高的缩放，使用其比例的\(log\)形式。

对于中心点平移，学习到的值需要添加宽和高的因子。这是由于，CNN具有尺度不变性，对于不同尺度的同一个目标，在最后的特征输出层学习到的特征是相同。如下图

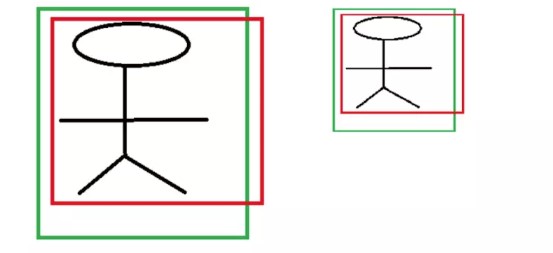
两个不同尺度的人，CNN提取的特征分别为\(\sigma_1,\sigma_2\)，这两个特征应该是相同的。假如边框回归学习到的映射为\(f\)，且\(f(\sigma)\)学习到的量。以\(x\)为例，\(x1,x2\)分别为两个人的Ground Truth，\(P_{1x},P_{2x}\)为两个候选区域的\(x\)坐标。假如，\(f(\sigma)\)直接表示平移的差值，则有\(x_1 - P_{1x} = f(\sigma_1),x2-P_{2x}=f(\sigma_2)\)。而\(\sigma_1,\sigma_2\)，这两个特征是相同的，则有\(f(\sigma_1) = f(\sigma_2)\)。故有\(x_1 - P_{1x} = x2-P_{2x}\)。从，上图看，这两个不同尺度的人的平移量，显然是不相同的。所以，将学习到的量作为坐标偏移显然是不可行的，R-CNN中给其添加了个尺度因子，也就是目标的宽和高。如下：
\[
f(\sigma_1) = x_1 - P_{1w}P_{1x} \\
f(\sigma_2) = x_2 - P_{2w}P_{2x}
\]

尺度（宽和高）的缩放，取其\(log\)形式。
需要学习得到宽和高的缩放因子，就需要将学习到的值限制为大于0，这里就取其\(exp(d_w(P)\)，来保证缩放因子都大于0.

总结

边框回归输入的是CNN学习到的候选区域的特征，以及候选区域的边框信息\((x,y,w,y)\)。通过学习得到映射\(d_x(P),d_y(P),d_w(P),d_h(P)\)。\(P_wd_x(P),P_hd_y(P)\)添加尺度因子后，作为坐标的平移；\(exp(d_w(P)),exp(d_h(P))\)取作为宽和高的缩放。