[BZOJ 1095] [ZJOI 2007] 捉迷藏

Description

传送门

Solution

先将原树转化成点分树：

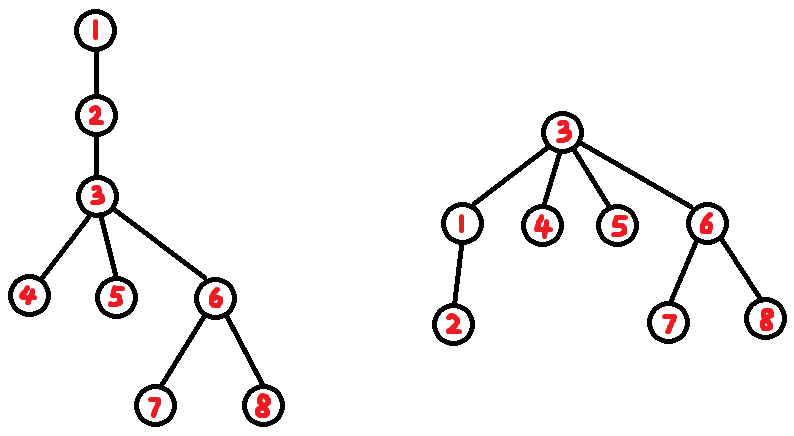
然后维护三个堆：

• \(c[i]\) 保存点分树中子树 \(i\) 中的黑色节点到 \(fa[i]\) 的距离；
• \(b[i]\) 保存点分树中 \(i\) 的每个儿子的 \(c[i]\) 的最大值；
• \(a\) 保存点分治的每个根 \(i\) 的最大答案。

注意重复修改可能会导致 \(b[i]\) 储存了两个在同一子树中的节点，在放入 \(a\) 前需判断。

Code

#include <queue>
#include <cstdio>
#include <algorithm>

const int N = 100002;
struct Edge { int v, nxt; } e[N << 1];
struct Pair {
    int x, y, z;
    bool operator < (const Pair & rhs) const {
        return x < rhs.x;
    }
};
int head[N], tot, fa[N], st[19][N << 1], rt, son[N], vis[N], col[N], dep[N], cnt, pos[N], siz[N], lg[N << 1];
std::priority_queue<Pair> a, b[N], c[N];

int read() {
    int x = 0; char c = getchar();
    while (c < '0' || c > '9') c = getchar();
    while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
    return x;
}
void adde(int u, int v) {
    e[++tot].nxt = head[u], head[u] = tot, e[tot].v = v;
}
void dfs(int u, int f) {
    dep[u] = dep[f] + 1, st[0][++cnt] = dep[u], pos[u] = cnt;
    for (int i = head[u]; i; i = e[i].nxt)
        if (e[i].v != f) dfs(e[i].v, u), st[0][++cnt] = dep[u];
}
void getrt(int u, int f) {
    siz[u] = 1, son[u] = 0;
    for (int i = head[u]; i; i = e[i].nxt) if (e[i].v != f && !vis[e[i].v])
        getrt(e[i].v, u), siz[u] += siz[e[i].v], son[u] = std::max(son[u], siz[e[i].v]);
    if ((son[u] = std::max(son[u], tot - siz[u])) < son[rt]) rt = u;
}
void solve(int u) {
    vis[u] = 1;
    for (int i = head[u]; i; i = e[i].nxt)
        if (!vis[e[i].v]) rt = 0, tot = siz[e[i].v], getrt(e[i].v, u), fa[rt] = u, solve(rt);
}
int get(int l, int r) {
    if (l > r) l ^= r, r ^= l, l ^= r;
    int k = lg[r - l + 1];
    return std::min(st[k][l], st[k][r - (1 << k) + 1]);
}
void insert(int u) {
    b[u].push((Pair){0, u, u});
    int v = u;
    while (fa[v]) c[v].push((Pair){dep[u] + dep[fa[v]] - (get(pos[u], pos[fa[v]]) << 1), u, u}), v = fa[v];
}
void update(int u, int f) {
    int v = u;
    if (f) b[u].push((Pair){0, u, u});
    while (v) {
        if (f && fa[v]) c[v].push((Pair){dep[u] + dep[fa[v]] - (get(pos[u], pos[fa[v]]) << 1), u, u});
        while (!c[v].empty() && col[c[v].top().y]) c[v].pop();
        if (!c[v].empty() && fa[v]) b[fa[v]].push(c[v].top());
        while (!b[v].empty() && col[b[v].top().y]) b[v].pop();
        if (b[v].empty()) { v = fa[v]; continue; }
        Pair x = b[v].top(), y;
        b[v].pop();
        if (b[v].empty()) { b[v].push(x), v = fa[v]; continue; }
        while (!b[v].empty() && (col[(y = b[v].top()).y] || dep[x.y] + dep[y.y] - (get(pos[x.y], pos[y.y]) << 1) < x.x + y.x)) b[v].pop();
        if (b[v].empty()) { b[v].push(x), v = fa[v]; continue; }
        a.push((Pair){x.x + y.x, x.y, y.y});
        b[v].push(x), v = fa[v];
    }
}
int main() {
    int n = read(); char opt[3];
    for (int i = 1, u, v; i < n; ++i) u = read(), v = read(), adde(u, v), adde(v, u);
    dfs(1, 0);
    for (int i = 2; i <= cnt; ++i) lg[i] = lg[i >> 1] + 1;
    for (int i = 1; (1 << i) <= cnt; ++i)
        for (int j = 1; j + (1 << i) - 1 <= cnt; ++j)
            st[i][j] = std::min(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
    tot = son[0] = n, getrt(1, 0), solve(rt), tot = n;
    for (int i = 1; i <= n; ++i) insert(i);
    for (int i = 1; i <= n; ++i) if (!c[i].empty() && fa[i]) b[fa[i]].push(c[i].top());
    for (int i = 1; i <= n; ++i) {
        Pair x = b[i].top();
        b[i].pop();
        if (b[i].empty()) { b[i].push(x); continue; }
        Pair y = b[i].top();
        b[i].push(x), a.push((Pair){x.x + y.x, x.y, y.y});
    }
    for (int m = read(); m; --m) {
        scanf("%s", opt);
        if (opt[0] == 'G') {
            if (!tot) puts("-1");
            else if (tot == 1) puts("0");
            else {
                while (col[a.top().y] || col[a.top().z]) a.pop();
                printf("%d\n", a.top().x);
            }
        } else {
            int x = read();
            if (!col[x]) col[x] = 1, --tot, update(x, 0);
            else col[x] = 0, ++tot, update(x, 1);
        }
    }
    return 0;
}