Codeforces #548 (Div2) - D.Steps to One（概率dp+数论）

Problem   Codeforces #548 (Div2) - D.Steps to One

Time Limit: 2000 mSec

Problem Description

Input

The first and only line contains a single integer mm (1≤m≤100000，1≤m≤100000).

Output

Print a single integer — the expected length of the array aa written as P⋅Q^−1(mod10^9+7)

Sample Input

4

Sample Output

333333338

题解：概率dp做的太少了，不会做。。。

　　首先是状态定义，dp[x]表示当前序列的gcd为x的情况下，还能添加数字个数的期望值，看了题解之后感觉这样很自然，但是自己想就想不到，有了这个定义之后状态转移就比较简单了，枚举下一个数字，根据期望的线性性质，有：

　　

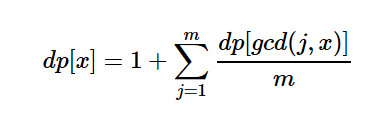
这样一来得到了一个O(n^2)的算法，显然不行，不过到这里的转化就很套路了，枚举gcd，式子化为：

　　

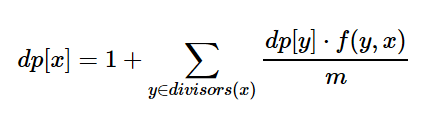
f(y, x)指的是和x的gcd是y的数有多少个（从1到m），预处理出1~m的约数，复杂度mlogm，这样不用根号m枚举约数，枚举y这一步题解中给出的均摊复杂度是logm，（不会证qwq，不过很多地方都是这么分析的），这样一来就只剩下f的求解了，设x = y * a，则和x的gcd为b的数必定可表达为 p = y * b且gcd(a, b) = 1，这样一来就相当于计算从1到m/y中和a互质的数的个数，也就是和a没有相同的质因子，打打表（看题解）可以发现在题目的范围内b的质因子数至多为6，容斥一下即可计数，最终复杂度O(mlogm*2^6*6)，是可以接受的。代码是看了题解的代码之后写的，主要学习这里质因数分解的操作。

 #include <bits/stdc++.h>

 using namespace std;

 #define REP(i, n) for (int i = 1; i <= (n); i++)
 #define sqr(x) ((x) * (x))

 const int maxn =  + ;
 const int maxm =  + ;
 const int maxs =  + ;

 typedef long long LL;
 typedef pair<int, int> pii;
 typedef pair<double, double> pdd;

 const LL unit = 1LL;
 const int INF = 0x3f3f3f3f;
 const LL mod = ;
 const double eps = 1e-;
 const double inf = 1e15;
 const double pi = acos(-1.0);

 LL pow_mod(LL x, LL n, LL mod)
 {
     LL base = x % mod;
     LL ans = ;
     while (n)
     {
         if (n & )
         {
             ans = ans * base % mod;
         }
         base = base * base % mod;
         n >>= ;
     }
     return ans % mod;
 }

 LL m, invm;
 unordered_map<int, int> prime[maxn];
 vector<LL> fact[maxn];
 bool is_prime[maxn];
 LL dp[maxn];

 void premanagement()
 {
     memset(is_prime, true, sizeof(is_prime));
     is_prime[] = is_prime[] = false;
     for (LL i = ; i < maxn; i++)
     {
         if (is_prime[i])
         {
             for (LL j = i; j < maxn; j += i)
             {
                 LL cnt = ;
                 LL tmp = j;
                 while (tmp % i == )
                 {
                     cnt++;
                     tmp /= i;
                 }
                 prime[j][i] = cnt;
                 is_prime[j] = false;
             }
             is_prime[i] = true;
         }
     }

     for (LL i = ; i < maxn; i++)
     {
         for (LL j =  * i; j < maxn; j += i)
         {
             fact[j].push_back(i);
         }
     }
 }

 LL cal(LL x, LL n)
 {
     vector<LL> a;
     LL curcnt = m / x;
     for (auto &item : prime[n])
     {
         if (!prime[x].count(item.first))
         {
             a.push_back(item.first);
             continue;
         }
         if (prime[x][item.first] == item.second)
         {
             continue;
         }
         else
         {
             a.push_back(item.first);
         }
     }

     LL sz = a.size();
     LL lim = m / x;
     for (LL sit = ; sit < (unit << sz); sit++)
     {
         LL tag = ;
         LL val = ;
         for (LL j = ; j < sz; j++)
         {
             if (sit & (unit << j))
             {
                 val *= a[j];
                 tag *= -;
             }
         }
         curcnt += tag * (lim / val);
     }
     return curcnt;
 }

 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie();
     //freopen("input.txt", "r", stdin);
     //freopen("output.txt", "w", stdout);
     cin >> m;
     invm = pow_mod(m, mod - , mod);
     premanagement();
     dp[] = ;
     for (LL i = ; i <= m; i++)
     {
         LL &ans = dp[i];
         ans = ;
         for (LL item : fact[i])
         {
             ans += cal(item, i) * dp[item] % mod * invm % mod;
             ans %= mod;
         }
         LL cnt = m / i;
         ans = ans * m % mod * pow_mod(m - cnt, mod - , mod) % mod;
     }
     LL ans = ;
     for (LL i = ; i <= m; i++)
     {
         ans = (ans + dp[i] * invm) % mod;
     }
     cout << ans << endl;
     return ;
 }