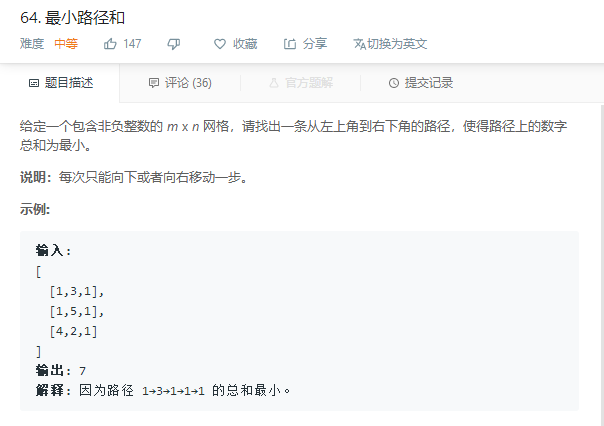
leetcode 64. 最小路径和Minimum Path Sum

很典型的动态规划题目

C++解法一：空间复杂度n²

 class Solution {
 public:
     int minPathSum(vector<vector<int>>& grid) {
         int m=grid.size(),n=grid[].size();
         int dp[m][n];
         dp[][]=grid[][];
         for(int i=;i<m;i++){
             dp[i][]=dp[i-][]+grid[i][];
         }
         for(int j=;j<n;j++){
             dp[][j]=dp[][j-]+grid[][j];
         }
         for(int i=;i<m;i++){
             for(int j=;j<n;j++){
                 dp[i][j]=min(dp[i-][j],dp[i][j-])+grid[i][j];
             }
         }
         return dp[m-][n-];
     }
 };

还可以简化一下空间，只用一个向量来进行运算；今天太累了，明天试着独立写一下；