[CQOI2011]放棋子 题解(dp+组合数学)

Description

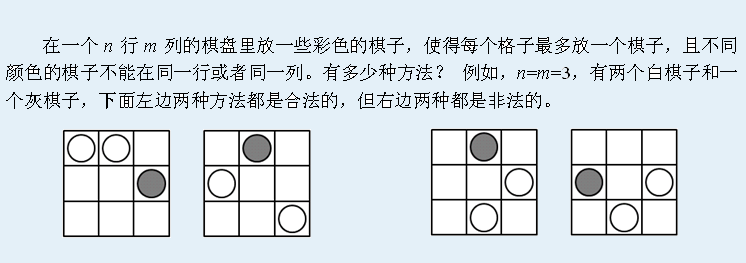
Input

输入第一行为两个整数n, m, c，即行数、列数和棋子的颜色数。

第二行包含c个正整数，即每个颜色的棋子数。

所有颜色的棋子总数保证不超过nm。

N,M<=30 C<=10 总棋子数有大于250的情况。

Output

输出仅一行，即方案总数除以 1,000,000,009的余数。

Sample Input

4 2 2
3 1

Sample Output

8

 

 

 

$Solution$

20%:爆搜，没甚么技术含量虽然我考场上还是没打对只骗到10分Orz

100%:

考虑dp

设$f[i][j][k]$为前k种颜色的棋子占任意i行j列的方案数

那么这个值肯定是前面一系列值的$\sum$

显然需要枚举两层$0<=l<i\ ,\ 0<=r<j$

之后就可以得到$f[l][r][k-1]$并将其累加

但因为我们设的状态是任意行列

需要在剩下的$n-l$行中选$i-l$行，列的话同理

所以要$*C_{n-l}^{i-l}*C_{m-r}^{j-r}$,

而且如果要转移过去还必须乘上某一种颜色占任意i行j列的方案数

这时设$g[i][j][k]$表示k枚同色棋子占任意i行j列的方案数

可得：

$f[i][j][k] = \sum _ {l = 0} ^ {i - 1} \sum _ {r = 0} ^ {j - 1} f[l][r][k - 1] * g[i - l][j - r][a[k]] * C_{n - l} ^ {i - l} * C_{m - r} ^ {j - r}$

正向求g比较困难，我们可以逆向思维，用所有方案数-不合法方案数之和

$g[i][j][k] = C_{i j} ^ {k} - \sum _ {l = 1} ^ {i} \sum _ {r = 1} ^ {j} g[l][r][k] * C_{i}^{l} * C_{j} ^ {r}$

最后统计$ans=\sum _ {i = 1} ^ {n} \sum _ {j = 1} ^ {m} f[i][j][c]$

收获:如果觉得状态设计得当，而缺少转移方程的某一部分时，不妨设一个辅助数组单独考虑。

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
int n,m,c,a[];
const ll mod=1e9+;
ll f[][][],g[][][],ans=,C[][];
int main()
{
    scanf("%d%d%d",&n,&m,&c);
    for(int i=;i<=c;i++)
        scanf("%d",&a[i]);
    if(c>min(n,m))
    {
        puts("");
        return ;
    }
    f[][][]=;C[][]=;
    for(int i=;i<=n*m;i++)
    {
        C[i][]=;
        for(int j=;j<=i;j++)
            C[i][j]=(C[i-][j]+C[i-][j-])%mod;
    }
    for(int k=;k<=c;k++)
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
            {
                if(a[k]>i*j)continue;
                ll res=;
                g[i][j][a[k]]=C[i*j][a[k]];
                for(int l=;l<=i;l++)
                    for(int r=;r<=j;r++)
                        if(l<i||r<j)
                            (res+=C[i][l]*C[j][r]%mod*g[l][r][a[k]]%mod)%=mod;
                g[i][j][a[k]]=(g[i][j][a[k]]-res+mod)%mod;
            }
    for(int k=;k<=c;k++)
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                for(int l=;l<i;l++)
                    for(int r=;r<j;r++)
                        (f[i][j][k]+=C[n-l][i-l]*C[m-r][j-r]%mod*f[l][r][k-]%mod*g[i-l][j-r][a[k]]%mod)%=mod;
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++)
            (ans+=f[i][j][c])%=mod;
    cout<<ans<<endl;
    return ;
}