Support Vector Machine(1):线性可分集的决策边界

与Logistuc Regression相比，SVM是一种优化的分类算法，其动机是寻找一个最佳的决策边界，使得从决策边界与各组数据之间存在margin，并且需要使各侧的margin最大化。比较容易理解的是，从决策边界到各个training example的距离越大，在分类操作的差错率就会越小。因此，SVM也叫作Large Margin Classifier。

最简单的情况是，在二维平面中的，线性可分情况，即我们的training set可以用一条直线来分割称为两个子集，如下图所示。而在图中我们可以看到，H2和H3都可以正确的将training set进行分类，但细细想来，使用H2进行分类的话，我们对于靠近蓝线的几个训练样例其实是不敢说100%的，但对于离蓝线最远的小球，我们却很有把握。这也是H3这条SVM红线出现的原因：尽量让两侧的训练样例远离决策边界，从而让我们的分类系统有把握对每个球Say Absolutely。

在Logistic Regression中，我们将类别y定义为0和1，从而把h(x)看做p(y=1)的概率，而在SVM里，我们将其定义为-1和+1。而我们所需要在n维空间中寻找的超平面，则被定义为：

由此，分类函数可以定义为：

将training example的坐标带入可以得到三种结果：f(x)=0,则该点处于决策平面上；f(x)>0,属于y=1类；f(x)<0，属于y=-1类。而对于每个训练样例，我们可以通过计算如下定义的“函数间隔”(functional margin)，来判断是否分类正确（数值为负则说明错误），以及通过数值大小看出测试点与决策平面的距离：

而真正表征SVM决策边界margin宽窄的，是上式中值最小的那个，也就是说，距离边界最近的点，其到边界的距离，决定了margin的大小。

而上式得出的函数间隔，实际上并不是该间隔真正的长度值，所以我们需要计算“几何间隔”(geometric margin)，即点到平面距离公式：

带入SVM公式，的几何间隔计算公式：

此时，我们想要做的事情是，最大化这个几何距离：

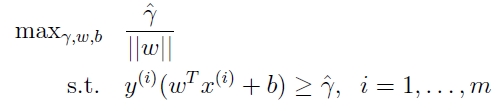
那么，如此看来，我们已经ok了，如下图：

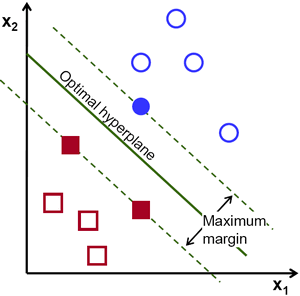
我们现在得到的三个hyperplane的方程为：

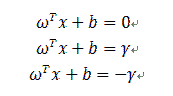
在这种情况下，margin是多少呢，根据平行线的距离公式：

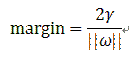
在这里其实我纠结了很长时间，因为很多课程从此就说的不太详细了，也许是我个人的数学水平较差吧，所以就花了很久去思考。首先，我们考虑到这个几何距离gamma，肯定是一个常数，因为当我们的f(x)确定，数据集确定以后，它就是离f(x)最近的点到f(x)=0这条直线的距离。那么，我们上述的三个方程，同时除以一个常数，一切会改变吗？首先，可以确定，3个方程一点也不会变，2x+4=6与x+2=3，是一样的对吗？那么我当时就想了，这波操作后，margin肯定会变的！实际上，由于gamma和w之间的线性关系，margin也是不变的，所以相当于，我们修改了w，从而消去了gammar。

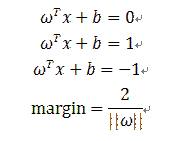
而单边的margin则等于总margin的一半：

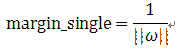
则问题转化为：

求解w的过程请见：Support Vector Machine(2)：求解线性可分SVM的最佳边界