学习笔记64_k邻近算法

1 .假定已知数据的各个属性值，以及其类型，例如：

电影名称	打斗镜头	接吻镜头	电影类别
m1	3	104	爱情片
m2	2	100	爱情片
m3	1	81	爱情片
m4	2	90	爱情片
w1	101	10	动作片
w2	99	5	动作片
w3	98	2	动作片

上述数据称为训练数据。

如果有新的电影， k1 , 18 , 90 ,未知

电影名称	与未知电影的距离
m1	20.5
m2	18.7
m3	19.2
m4	21
w1	115.3
w2	117.4
w5	118.9

距离 ： 通过一定的计算方法获得 ， 总体来说，距离 = f (k1打斗镜头，k1接吻镜头，m1打斗镜头，m1接吻镜头)

如果 k1与 某些电影 最接近，这里，就是3个电影最接近， 所以K1为爱情片，这里K可以为3，或2 ，或1都行。

***如果出现了距离为 50的片1部，它既不是爱情片，也不是动作片，那么，由于

K邻近算法：

1.存在一个样本数据集合， 且样本中，每个数据都存在标签（已经分好类）

2.输入没有标签的新数据后（没有分类的），将新数据的每个特征值，使用一定的办法，与样本中的特征进行比较，然后提取出那些最近似（距离最小）的数据的类型，其中出现最多的类型，作为自己的类型。

***** 一般来说，如果有大量的数据的时候，只需要遍历出K个距离足够小的样本，然后从样本中，选择出现类型最多的分类，作为新数据的分类。

关键点：

1.K的取值（根据数据量，以及各个分类占有的百分比取）。

2.距离如何计算。

3.如何界定距离足够小。

*************************************************************************************************

使用K近邻算法，进行简单的图形识别：

简单： 要识别的东西的特征比较明显；图片颜色有比较强的对比度；图片刚好括着要识别的东西；要识别的东西放得比较正 等等。

***若果不满足简单，那么就需要预处理，将图片简单化*****

假设有图片：

图片的数据是像素，假设图片的数据格式：

（r11,g11,b11）	(r12,g12,b12)	(r13,g13,b13)	...
（r21,g21,b21）	...	...	...
（r31,g31,b31）	...	...	...
...	...	...	...

这样的数据结构，假设有大量图片，对每个图片：

第一步：读取图片数据，然后上述的数据结构。

第二步：归一化，如上图，颜色可以分为2类，选择 这个颜色的 RGB运算值为1，其他为0

*实际上，每个训练数据的图片，颜色可能都是不一样的，可以使用聚类：

情况可能有如下： 1. 只有两种颜色，如果某种颜色的比例占少数，那么这个颜色运算值应该为1；

　　　　　　　　 2. 三种以上颜色，如果某种颜色的比例占多数，那么这个颜色运算值应该为1；

（归一化的算法很多。）

第三步：形成   特征-分类：

*第n行值，是指第n行中，1的总数。

第1行值	第2行值	第3行值	...	数字类型
5	9	10	...	2
5	5	5	...	1
6	8	11	...	2
...	...	...	...	3
...	...	...	...	4
...	...	...	...	...

算法使用：

1.如果要识别新的图片，首先要执行上面 一，二，三部；

2.求距离：

d = Math.sqrt( d1² + d2² + ............ )

遍历出K个距离足够小的 样本

3. 在K个样本中，找出“数字类型”出现最多的 类型，作为 新的图片 所识别的数字。

除了使用MSQ（均方差，也就是d平方）的方法外，对于样本属于哪一类，还有使用夹角来衡量：

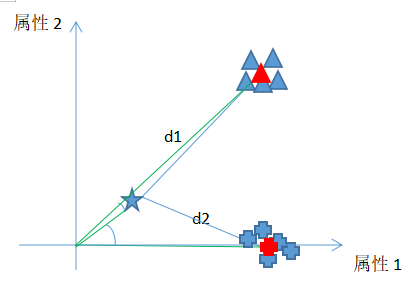
假如属性1为数学成绩，属性2位语文成绩，三角形为“均衡生”，而加号为“偏科生”，那么，要认定星号样本属于“均衡生”还是“偏科生”，

显然应该是“均衡生”，但是d1>d2，所以用空间夹角最好（联想向量点积计算）。

补充一点，这个“距离”，其实可以联想到神经网络中的“损失函数”