算法设计（动态规划实验报告） 基于动态规划的背包问题、Warshall算法和Floyd算法

一、名称

动态规划法应用

二、目的

1.掌握动态规划法的基本思想；
2.学会运用动态规划法解决实际设计应用中碰到的问题。

三、要求

1．基于动态规划法思想解决背包问题（递归或自底向上的实现均可）；
2．实现基于动态规划法思想的Warshall算法和Floyd算法。

四、仿真内容

1．基于动态规划法思想解决背包问题

1.1、解决背包问题的伪代码描述

算法 MFKnapsack(i,j)
//对背包问题实现记忆功能方法
//输入：一个非负整数i表示先考虑的物品数量，一个非负整数j表示背包的承受重量
//输出：前i个物品的最最优可行子集的价值
If F[I,j]<0
  If j<MFKnapsack(i-1,j)
     Value←MFKnapsack(i-1,j)
 Else
value←max(MFKnapsack(i-1,j),
          Values[i]+MFKnapsack(i-1,j-Weights[i]))
F[I,j] ←value
Return F[I,j]

2.2、解决背包问题的源代码实现

package com.zyz.back;

import java.util.Random;

public class BackQuestion {

    public static int knaspace(int[] weight, int[] value, int maxweight) {
        // 参数 i为放入前i个物体，j为背包的最大承重量。
        int n = weight.length;// 放入商品的质量
        int[][] maxvalue = new int[n + 1][maxweight + 1];// 背包最大的价值。放入第i个在当前背包的最大价值

        int[][] help = new int[n][2];//用来记录商品的价值和质量

        for (int i = 0; i < maxweight + 1; i++) { // 第0个商品放入背包,最大价值为0
            maxvalue[0][i] = 0;
        }

        for (int i = 0; i < n + 1; i++) {
            maxvalue[i][0] = 0;// 第i个商品放入背包为0的书包，最大价值为0
        }

//    //参数 i为放入前i个物体，j为背包的最大承重量。

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= maxweight; j++) {// 背包容量逐渐增加
                maxvalue[i][j] = maxvalue[i - 1][j];// 将较小的数赋值

                if (weight[i - 1] <= j) {// 待放入的物品质量小于背包的容量
                    // 放入第i个商品的价值maxvalue[i-1][j-weight[i-1]+value[i-1]

                    if (maxvalue[i - 1][j - weight[i - 1]] + value[i - 1] > maxvalue[i][j]) {
                        maxvalue[i][j] = maxvalue[i - 1][j - weight[i - 1]] + value[i - 1];
                    }

                }

            }

        }
        return maxvalue[n][maxweight];
    }

    public static void main(String[] args) {
        int maxweight = 14;// 书包的容量
        // 随机生成数组
        int W = 15;
        int V = 25;
        Random random = new Random();
        int[] weight = new int[20];
        int[] value = new int[20];

        // 随机给商品附加质量
        for (int i = 0; i < weight.length; i++) {

                weight[i] = random.nextInt(W);
            if(weight[i]==0){
                weight[i]=2;
            }

        }

        System.out.println("商品的质量：");
        for (int i = 0; i < weight.length; i++) {
            System.out.print(weight[i] + " ");
        }

        System.out.println();
        // 随机给商品附加值
        System.out.println("商品的价值：");
        for (int i = 0; i < value.length; i++) {
            value[i] = random.nextInt(V);
            if(value[i]==0){
                value[i]=3;
            }
        }

        for (int i = 0; i < value.length; i++) {
            System.out.print(value[i] + " ");
        }
        long startTime=System.currentTimeMillis();
        int result = knaspace(weight, value, maxweight);
        long endTime=System.currentTimeMillis();
        long time=endTime-startTime;
        System.out.println("\n背包最大的价值：" + result);
        System.out.println("数据大小："+value.length+"  耗时："+time+"毫秒");

    }

}

2.3、时间效率分析

动态法实现背包问题，动态的增加背包的容量，保证放入的商品价值始终是最大的。判断每次新放入的商品和之前放入的商品价值之间的价值比较。比之前的价值大则放入背包。小则不放入。时间效率为Tn=(n).

2．实现基于动态规划法思想的warshall

2.1、warshall算法的伪代码描述

算法 Warshall(A[1…n,1…n])
//实现计算传递闭包的Warshall算法
//输入：包括n个顶点有向图的邻接矩阵A
//输出：该有向图的传递闭包
R(0)←A
For k←1 to n do
   For i←1 to n do
     For j←1 to n do
R(k)[I,j] ←R(I,j) or R(k-1)[I,k] and R(k-1)[k,j]
Return R(n)

2.2、warshall算法的源代码实现

package com.zyz.comlate;

import java.util.Scanner;

public class Warshall {

    public void warshall(int a[][]) {
        for (int k = 0; k < a.length; k++) {//求取最终的封闭包通过R0求R1，通过R1求R2。。。。直到最后
            for (int j = 0; j < a.length; j++) {//用来判断a[j][i]是否连通
                if (a[k][j] == 1) {
                    for (int i = 0; i < a.length; i++) {
                        if (a[i][k] == 1) {
                            a[j][i] = 1;
                        }
                    }
                }
            }
        }

    }

    //打印
    public void print(int[][] a) {
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length; j++) {
                System.out.print(a[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        System.out.println("请输入阶数：");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int[][] a = new int[n][n];
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length; j++) {
                if (i == j) {
                    a[i][j] = 0;
                } else {
                    a[i][j] = (Math.random() > 0.6 ? 1 : 0);
                }

            }
        }

        Warshall warshall = new Warshall();
        System.out.println("原始数据：");
        warshall.print(a);
        System.out.println("处理后的数据：");

        long startTime=System.currentTimeMillis();
        warshall.warshall(a);
        long endTime=System.currentTimeMillis();
        long time=endTime-startTime;
        warshall.print(a);
        System.out.println("耗时："+time+"毫秒");

    }

}

2.3、时间效率分析

T=O(nnn)

3．实现基于动态规划法思想的Floyd算法

3.1、Floyd算法的伪代码描述

算法：Floyd(W[1..n],[1..n]
//实现计算完全最短路径的Floyd算法
//输入：不包含长度为负的回路的图的权重矩阵W
//输出：包含最短路径长度的距离矩阵
D←W
For k←1 to n do
 For i←1 to n do
  For j←1 to n do
   D[I,j] ←min{D[I,j],D[I,j]+D[k,j]}
Return D

3.2、Floyd算法的源代码实现

package com.zyz.comlate;

import java.util.Scanner;

public class Floyd {

    public void floyd(int a[][]) {

        for (int k = 0; k < a.length; k++) {//求第Rk次的封闭包
            for (int j = 0; j < a.length; j++) {//判断第Rk次的位置的最短路径。每次增加一个新的顶点。
                for (int i = 0; i < a.length; i++) {
                    if (a[j][i] > (a[j][k] + a[k][i])) {//新的路径比原先的路径更加短，则将最短路径写入
                        a[j][i] = a[j][k] + a[k][i];
                    }
                }
            }
        }
    }

    // 打印
    public void print(int[][] a) {
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length; j++) {
                if (a[i][j] == 3 || a[i][j] == 7 || a[i][j] == 6 || a[i][j] == 5 || a[i][j] == 9) {
                    System.out.print("∞" + " ");
                } else {
                    System.out.print(a[i][j] + " ");
                }
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        System.out.println("请输入矩阵阶数：");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int[][] a = new int[n][n];
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length; j++) {
                if (i == j) {
                    a[i][j] = 0;
                } else {
                    a[i][j] = (int) (Math.random() * 10);
                }

            }
        }
        Floyd floyd = new Floyd();
        System.out.println("原始数据：");
        floyd.print(a);
        System.out.println("处理后的数据：");
        long startTime = System.currentTimeMillis();
        floyd.floyd(a);
        long endTime = System.currentTimeMillis();
        long time = endTime - startTime;
        floyd.print(a);
        System.out.println("耗时：" + time + "毫秒");

    }

}

3.3、Floyd算法的时间效率分析

T=O(nnn)

4、运行结果

4.1、基于动态规划法思想解决背包问题

1）背包问题测试结果

4.2、Warshall算法的测试用例结果截图

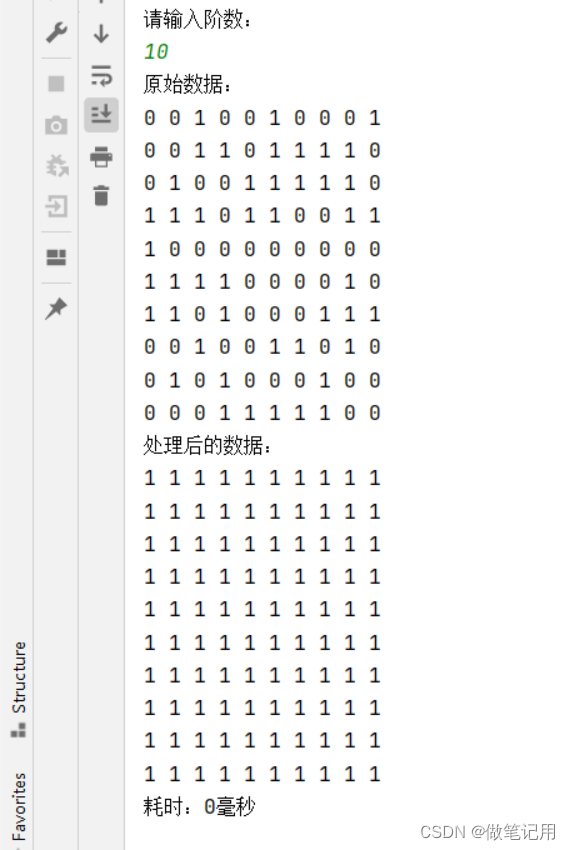
4.3、Floyd算法的测试用例结果截图

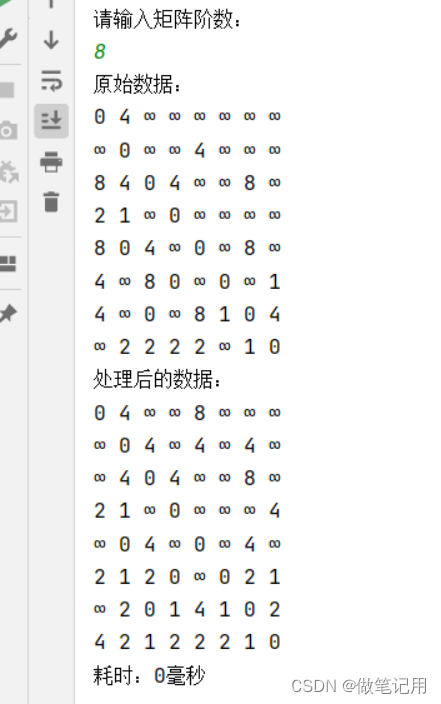
5、小结

通过本次实验我了解到动态化和基于动态规划法思想的Warshall算法和Floyd算法使用。我对动态规划法有了更加深入的了解，通过把一个大的问题分级减少为若干个子问题，通过对子问题的求解最终达到求解问题的结果。