「学习笔记」重修 FHQ-treap

无旋 treap 的操作方式使得它天生支持维护序列、可持久化等特性。

无旋 treap 又称分裂合并 treap。它仅有两种核心操作，即为 分裂 与 合并。通过这两种操作，在很多情况下可以比旋转 treap 更方便的实现别的操作。

变量与宏定义

#define ls ch[u][0]
#define rs ch[u][1]
int cnt, rt, top;
int ch[N][2], siz[N], val[N], pai[N], rub[N];

ls: 左孩子；

rs: 右孩子；

cnt: 计数器；

rt: 根；

top: “垃圾桶”的栈顶

ch: 左右孩子，0 为左孩子，1 为右孩子；

siz: 子树大小；

val: 键值；

pai：随机的值，用于堆排序；

rub: 垃圾桶。

操作

• 按权值分裂

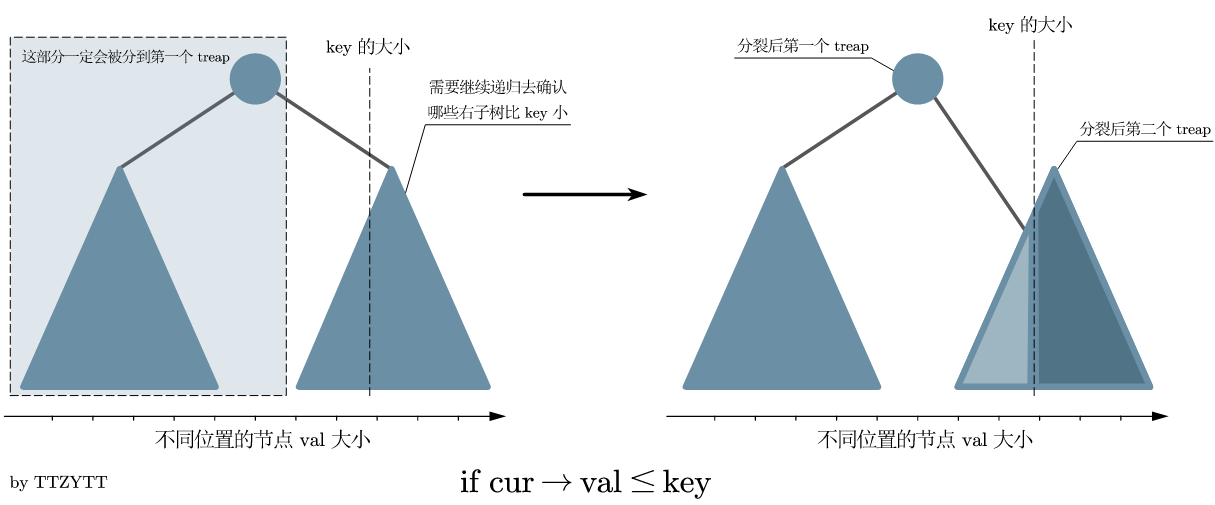
给定一个权值，小于等于该权值的分裂到左边，大于该权值的分裂到右边。

在分裂过程中也要维护二叉搜索树的性质，即当前节点左子树任意一个节点的 val 都小于等于当前节点的 val，右子树任意一个节点的 val 都大于当前节点的 val。

void split1(int u, int c, int &x, int &y) { // 按照权值分裂
	if (u == 0) {
		x = y = 0;
		return ;
	}
	if (val[u] <= c) {
		x = u;
		split1(rs, c, rs, y);
	}
	else {
		y = u;
		split1(ls, c, x, ls);
	}
	pushup(u);
}

u: 当前节点；

c: 给定分裂的权值；

x: 要分裂成的左树；

y: 要分裂成的右树。

if (val[u] <= v) {
	x = u;
	split1(rs, c, rs, y);
}

如果当前节点的 val 小于 \(c\)，那么久把当前节点连带它的左子树一起放到 x 上，接下来向右子树搜索，若还有要接到 x 上的节点，就接到 x 的右子树上，以此来维护二叉搜索树的性质。如下图（图片来自 \(\text{OI wiki}\)）。



pushup(u); 为更新函数，后面会写。

• 按子树大小分裂

将前 \(k\) 个节点分成一棵树，其他节点分成一棵树。

void split2(int u, int k, int &x, int &y) { // 按照子树大小分裂
	if (u == 0) {
		x = y = 0;
		return ;
	}
	pushup(u);
	if (siz[ls] + 1 <= k) {
		x = u;
		split2(rs, k - siz[ls] - 1, rs, y);
	}
	else {
		y = u;
		split2(ls, k, x, ls);
	}
	pushup(u);
}

if (siz[ls] + 1 <= k) {
	x = u;
	split2(rs, k - siz[ls] - 1, rs, y);
}

siz[ls] + 1 是当前的节点和它的左子树的总 siz，siz 小于 \(k\)，放到左子树，x 变成 rs。

• 合并

两棵树合并，如果一棵树为空，则直接合并，否则，根据 pai 的大小来判断谁是父节点。

小根堆 pai 小的为父节点，大根堆 pai 大的为父节点。

int merge(int x, int y) {
	if (!x || !y) {
		return x + y;
	}
	if (pai[x] < pai[y]) {
		ch[x][1] = merge(ch[x][1], y);
		pushup(x);
		return x;
	}
	else {
		ch[y][0] = merge(x, ch[y][0]);
		pushup(y);
		return y;
	}
}

注意，合并时 x 是左树，y 是右树，一定要保证左右顺序！

• 更新信息

void pushup(int u) {
	siz[u] = siz[ls] + siz[rs] + 1;
	return ;
}

• 删除节点

这里是删除已知权值的点，若存在多个则只删一个，删除的点将放进“垃圾桶”，当有些节点要创建时先从“垃圾桶”里找可用的点，节省空间。

void del(int c) {
	int t1, t2, t3;
	split1(rt, c, t1, t2);
	split1(t1, c - 1, t1, t3);
	rub[++ top] = t3;
	t3 = merge(ch[t3][0], ch[t3][1]);
	rt = merge(merge(t1, t3), t2);
}

t3 = merge(ch[t3][0], ch[t3][1]);
rt = merge(merge(t1, t3), t2);

由于相同权值的节点只删了一个，t3 可能不为空，所以还要再合并起来.

• 创建新节点

int New(int c) {
	int u;
	if (!top) {
		u = ++ cnt;
	}
	else {
		u = rub[top];
		top --;
	}
	val[u] = c;
	siz[u] = 1;
	pai[u] = rand();
	ls = 0, rs = 0;
	return u;
}

if (!top) {
	u = ++ cnt;
}
else {
	u = rub[top];
	top --;
}

如果“垃圾桶”里还有点，那就将这些点回收利用，否则就开新节点。

• 插入

先将树按照权值分裂，然后将新节点依次与左树和右树合并，merge 的顺序不要搞反了。

void insert(int c) {
	int t1, t2;
	split1(rt, c, t1, t2);
	rt = merge(merge(t1, New(c)), t2);
}

• 查询排名

按照权值分裂，返回 siz[ls] + 1。

int ranking(int c) {
	int t1, t2, k;
	split1(rt, c - 1, t1, t2);
	k = siz[t1] + 1;
	rt = merge(t1, t2);
	return k;
}

• 查询第 \(K\) 大

按照子树大小分裂即可

int K_th(int k) {
	int t1, t2, t3, c;
	split2(rt, k, t1, t2);
	split2(t1, k - 1, t1, t3);
	c = val[t3];
	rt = merge(merge(t1, t3), t2);
	return c;
}

• 查找前驱

int pre(int c) {
	int t1, t2, t3, k;
	split1(rt, c - 1, t1, t2);
	split2(t1, siz[t1] - 1, t1, t3);
	k = val[t3];
	rt = merge(merge(t1, t3), t2);
	return k;
}

• 查找后继

int nxt(int c) {
	int t1, t2, t3, k;
	split1(rt, c, t1, t2);
	split2(t2, 1, t2, t3);
	k = val[t2];
	rt = merge(t1, merge(t2, t3));
	return k;
}

---

由于 FHQ 的核心操作是分裂与合并，所以，不同于 treap，它可以方便的进行区间操作。

模板

struct FHQ {
	int cnt, rt, top;
	int ch[N][2], siz[N], val[N], pai[N], rub[N];

	void pushup(int u) {
		siz[u] = siz[ls] + siz[rs] + 1;
		return ;
	}

	int New(int c) {
		int u;
		if (!top) {
			u = ++ cnt;
		}
		else {
			u = rub[top];
			top --;
		}
		val[u] = c;
		siz[u] = 1;
		pai[u] = rand();
		ls = 0, rs = 0;
		return u;
	}

	void split1(int u, int c, int &x, int &y) { // 按照权值分裂
		if (u == 0) {
			x = y = 0;
			return ;
		}
		if (val[u] <= c) {
			x = u;
			split1(rs, c, rs, y);
		}
		else {
			y = u;
			split1(ls, c, x, ls);
		}
		pushup(u);
	}

	void split2(int u, int k, int &x, int &y) { // 按照子树大小分裂
		if (u == 0) {
			x = y = 0;
			return ;
		}
		pushup(u);
		if (siz[ls] + 1 <= k) {
			x = u;
			split2(rs, k - siz[ls] - 1, rs, y);
		}
		else {
			y = u;
			split2(ls, k, x, ls);
		}
		pushup(u);
	}

	int merge(int x, int y) {
		if (!x || !y) {
			return x + y;
		}
		if (pai[x] < pai[y]) {
			ch[x][1] = merge(ch[x][1], y);
			pushup(x);
			return x;
		}
		else {
			ch[y][0] = merge(x, ch[y][0]);
			pushup(y);
			return y;
		}
	}

	void insert(int c) {
		int t1, t2;
		split1(rt, c, t1, t2);
		rt = merge(merge(t1, New(c)), t2);
	}

	void del(int c) {
		int t1, t2, t3;
		split1(rt, c, t1, t2);
		split1(t1, c - 1, t1, t3);
		rub[++ top] = t3;
		t3 = merge(ch[t3][0], ch[t3][1]);
		rt = merge(merge(t1, t3), t2);
	}

	int ranking(int c) {
		int t1, t2, k;
		split1(rt, c - 1, t1, t2);
		k = siz[t1] + 1;
		rt = merge(t1, t2);
		return k;
	}

	int K_th(int k) {
		int t1, t2, t3, c;
		split2(rt, k, t1, t2);
		split2(t1, k - 1, t1, t3);
		c = val[t3];
		rt = merge(merge(t1, t3), t2);
		return c;
	}

	int pre(int c) {
		int t1, t2, t3, k;
		split1(rt, c - 1, t1, t2);
		split2(t1, siz[t1] - 1, t1, t3);
		k = val[t3];
		rt = merge(merge(t1, t3), t2);
		return k;
	}

	int nxt(int c) {
		int t1, t2, t3, k;
		split1(rt, c, t1, t2);
		split2(t2, 1, t2, t3);
		k = val[t2];
		rt = merge(t1, merge(t2, t3));
		return k;
	}
};