基于python的数学建模---最小二乘拟合

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
from matplotlib.pylab import mpl
 
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
 
# 计算以p为参数的直线与原始数据之间误差
def f(p):
    k, b = p
    return Y - (k * X + b)
 
if __name__ == '__main__':
    X = np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
    Y = np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
    # leastsq使得f的输出数组的平方和最小，参数初始值为[1,0]
    r = leastsq(f, [1, 0])  # 数初始值可以随便设个合理的
    k, b = r[0]
    x = np.linspace(0, 10, 1000)
    y = k * x + b
 
    # 画散点图，s是点的大小
    plt.scatter(X, Y, s=100, alpha=1.0, marker='o', label=u'数据点')
    # 话拟合曲线，linewidth是线宽
    plt.plot(x, y, color='r', linewidth=2, linestyle="-", markersize=20, label=u'拟合曲线')
    plt.xlabel('安培/A')
    plt.ylabel('伏特/V')
    plt.legend(loc=0, numpoints=1)  # 显示点和线的说明
    # plt.plot(X, Y)
    plt.show()
 
    print('k = ', k)
    print('b = ', b)

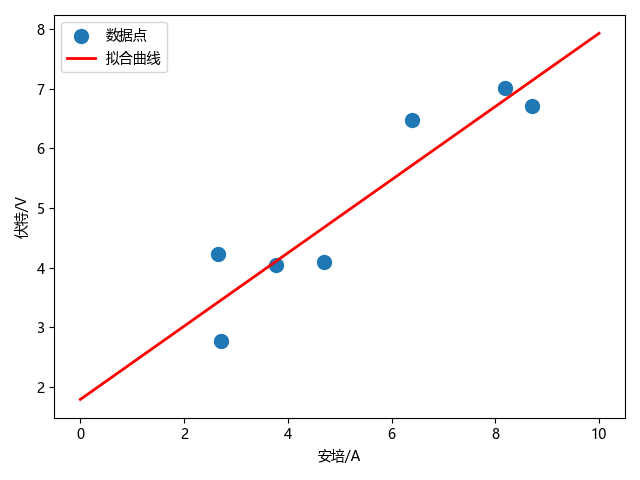
k = 0.6134953491930442
b = 1.794092543259387

• 下面是用anaconda写的

import numpy as np
import matplotlib.pyplot as plt
 
np.set_printoptions(suppress=True) # 取消科学计数法
 
x = np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
y = np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
 
plt.figure()
plt.scatter(x,y)
plt.show()

from scipy.optimize import leastsq
 
def error(p,x,y):
    return p[0]*x + p[1] - y
 
p0 = [2,2] #设置初始值
 
res = leastsq(error,p0,args=(x,y))
 
k,b = res[0]
print(k)
print(b)

0.6134953485739788
1.7940925393506084

x1 = np.linspace(0,9,1000)
y1 = k*x1+b
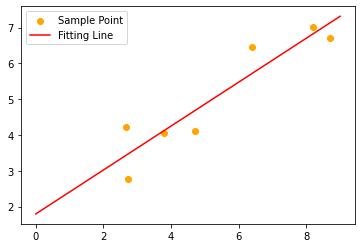
plt.scatter(x,y,color= 'orange',label = 'Sample Point')
plt.plot(x1,y1,color= 'red',label = 'Fitting Line')
plt.legend()
plt.show()