目录

一、Erlang环境部署

1、百度搜索"Erlang",或者访问网址:https://www.erlang.org/,找到DOWNLOAD双击进入。

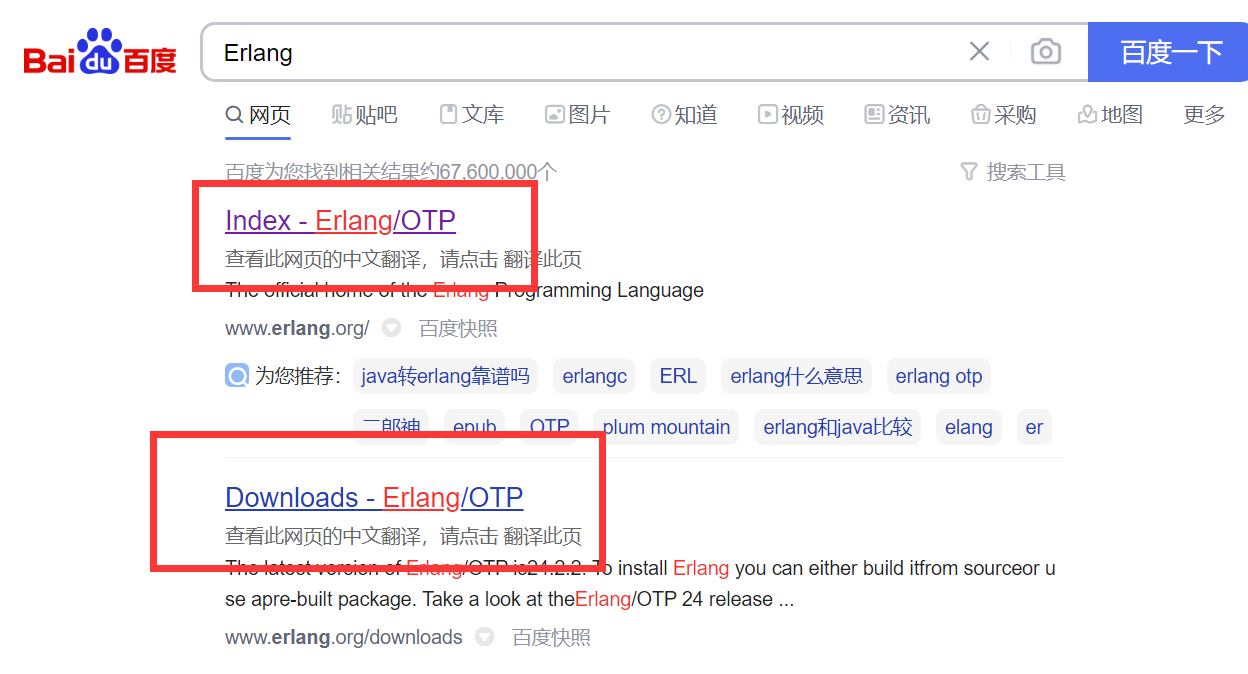
2、找到支持的windows下载位置，双击下载

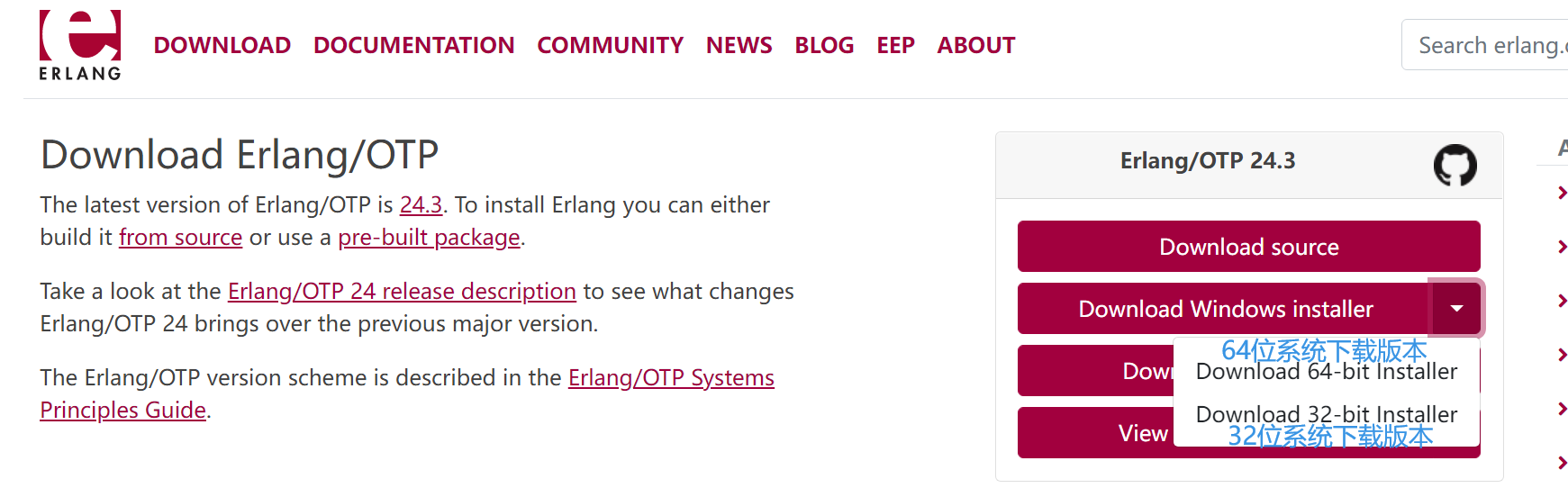
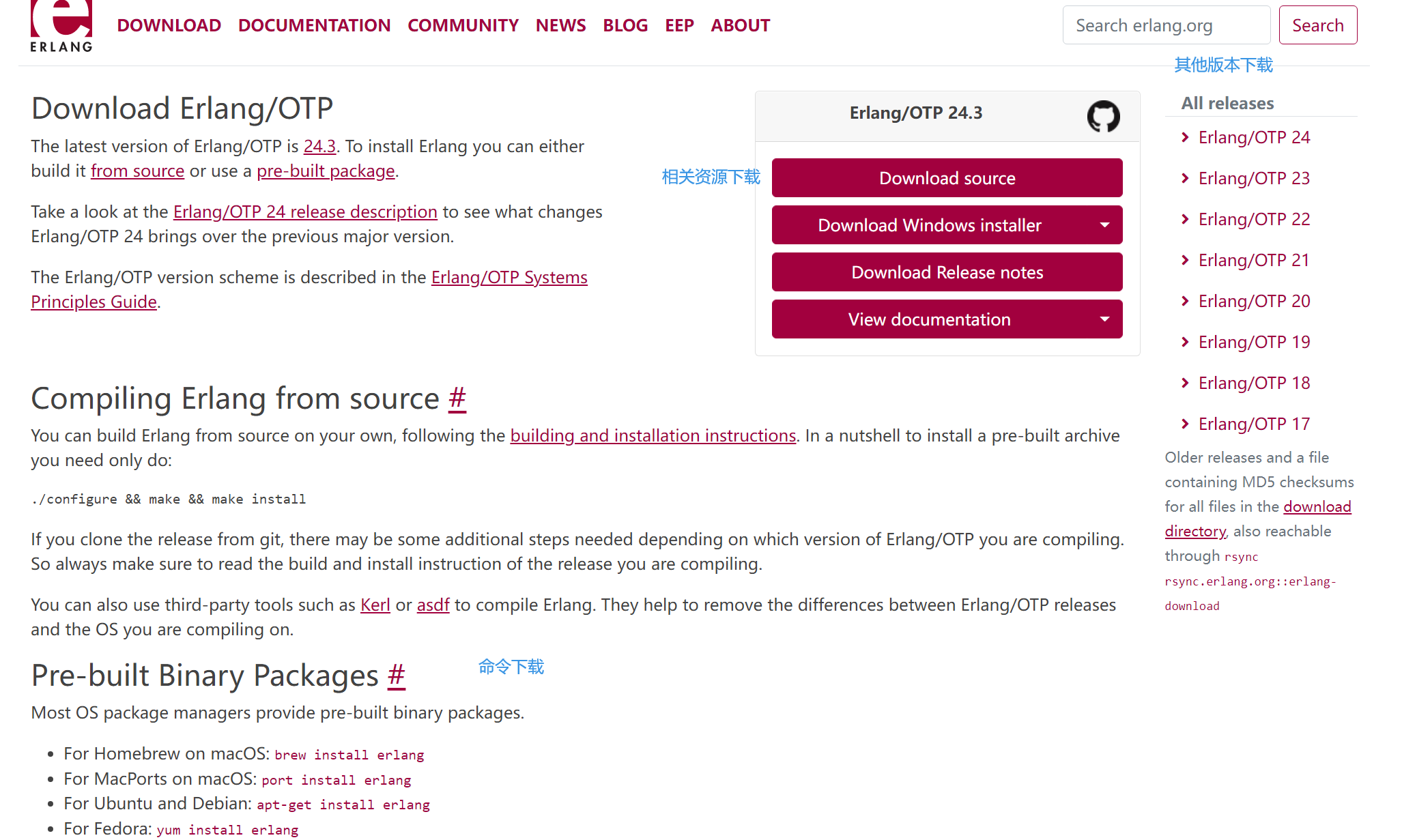
3、找到文件下载位置，双击安装，接着点击next。

4、选择安装路径，点击next。

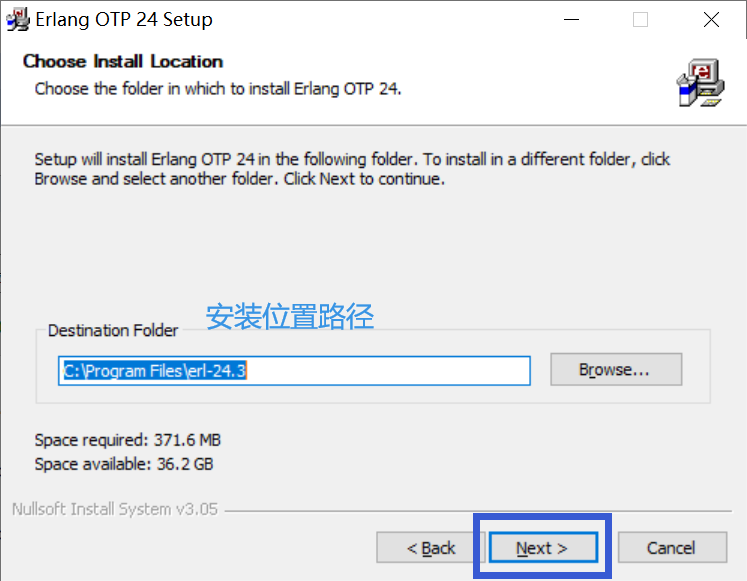
5、选择文件夹名称，点击Insatall。

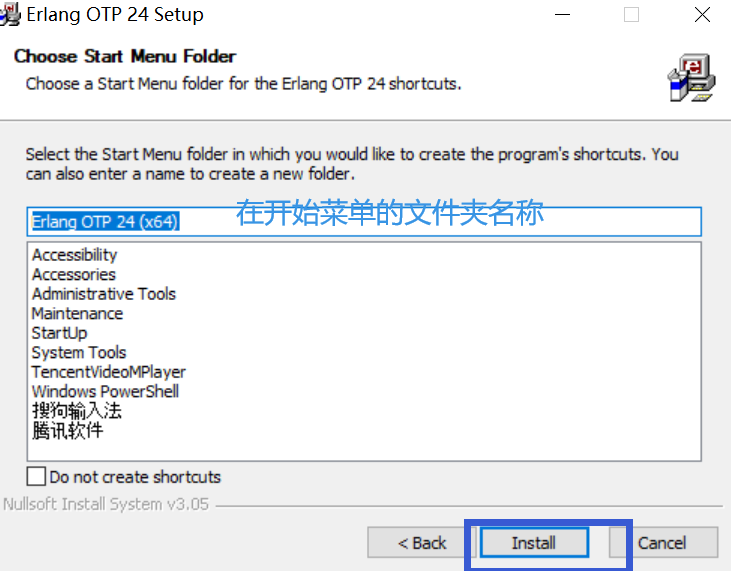
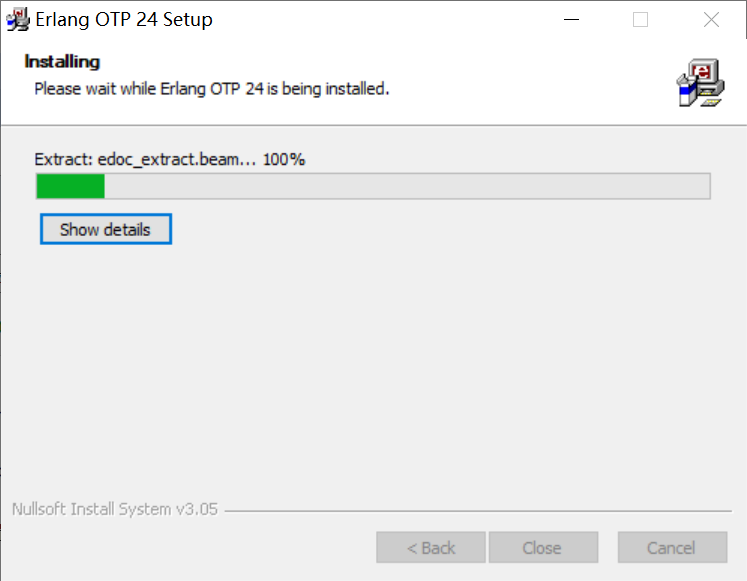
  • 新系统提示安装这个插件，选择安装即可。

6、安装成功，点击close。

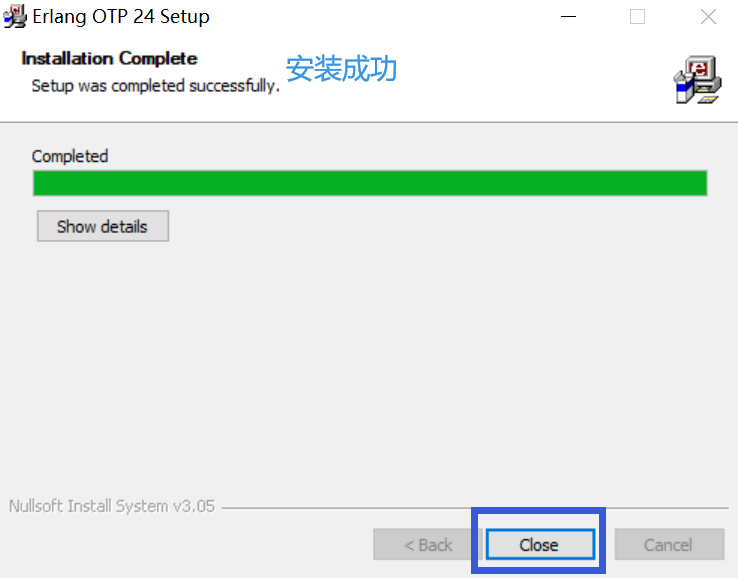
  • 找到本地位置

7、此电脑-->右键属性，单击属性，选择高级系统设置。

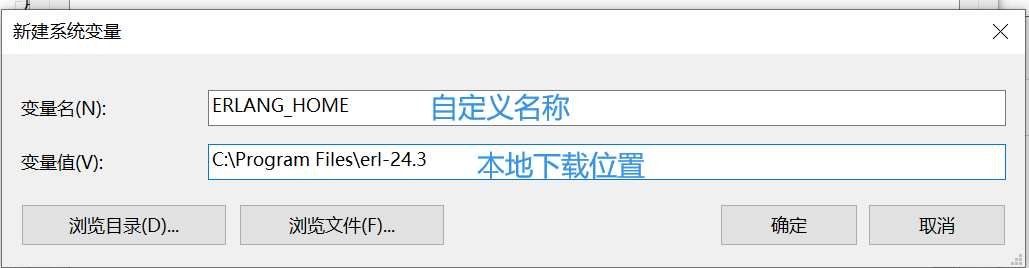
8、弹出框中，选择环境变量，找到系统变量，单击新建，填写信息，点击确定

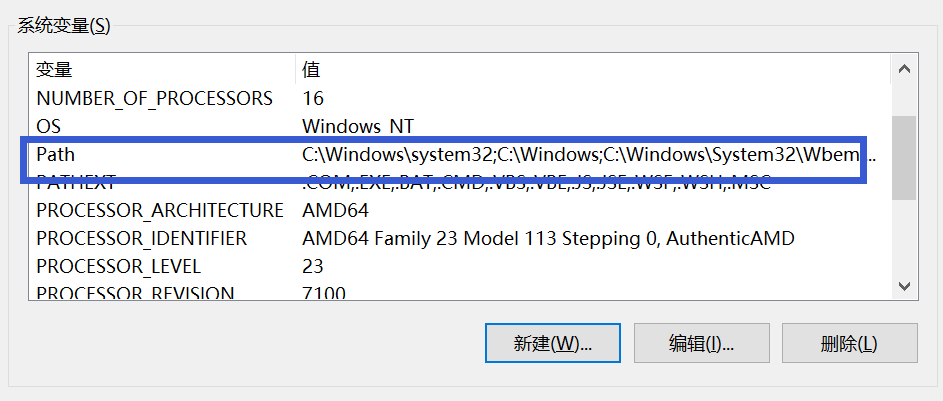
9、在系统变量中找到path，双击打开，填入信息，选择确定

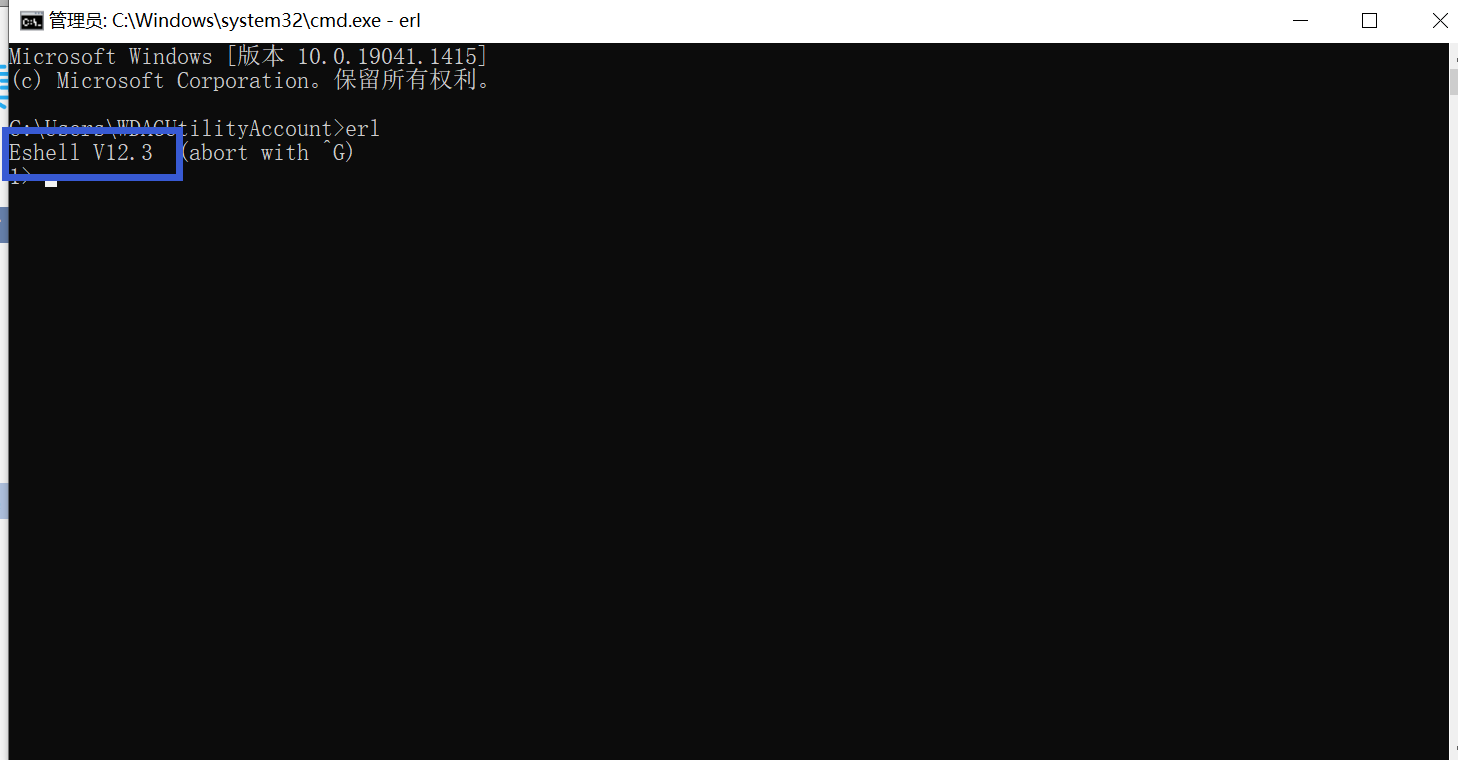
10、windows + R弹出命令窗口，输入cmd进入命令模式，输入erl，返回版本信息即为成功

二、RabbitMQ安装

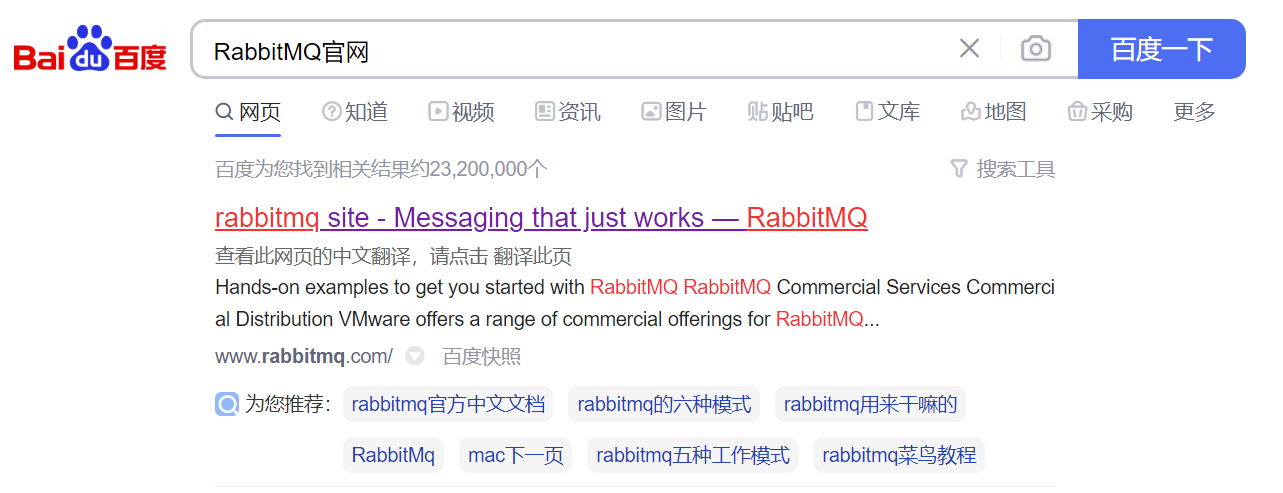
1、搜索百度"RabbitMQ官网",搜到如下图的,双击进入,网址:https://www.rabbitmq.com/

2、进入主页，选择GET STARTED，选择Download + Installation进入，点击右侧下载，

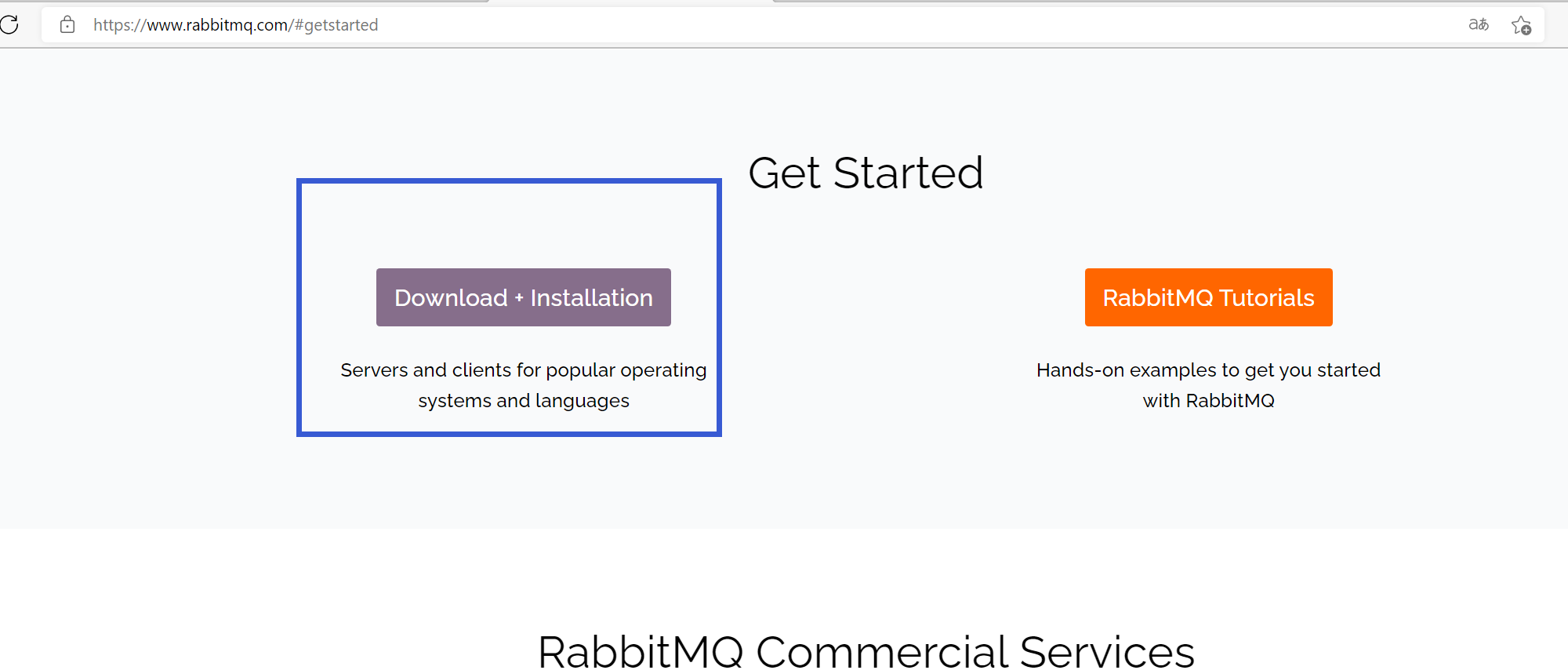
  • 或者下拉找到windows位置。

3、找到下载的位置，双击进行安装，选择组件（默认即可），点击next

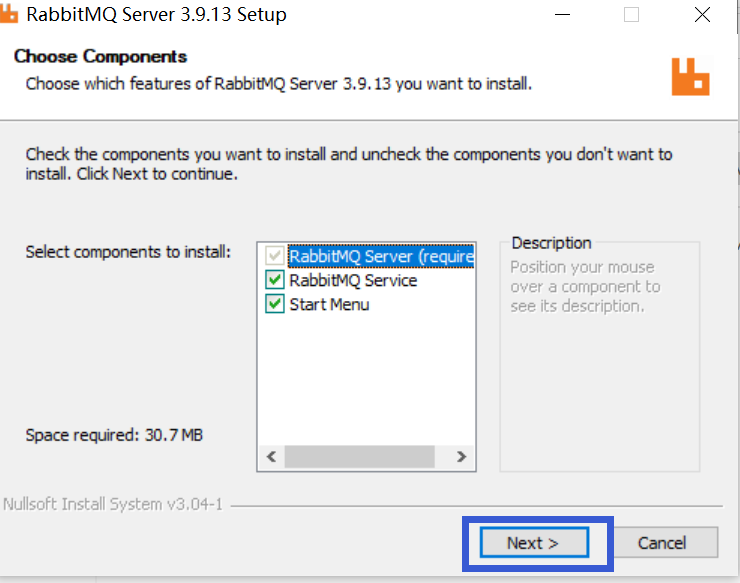
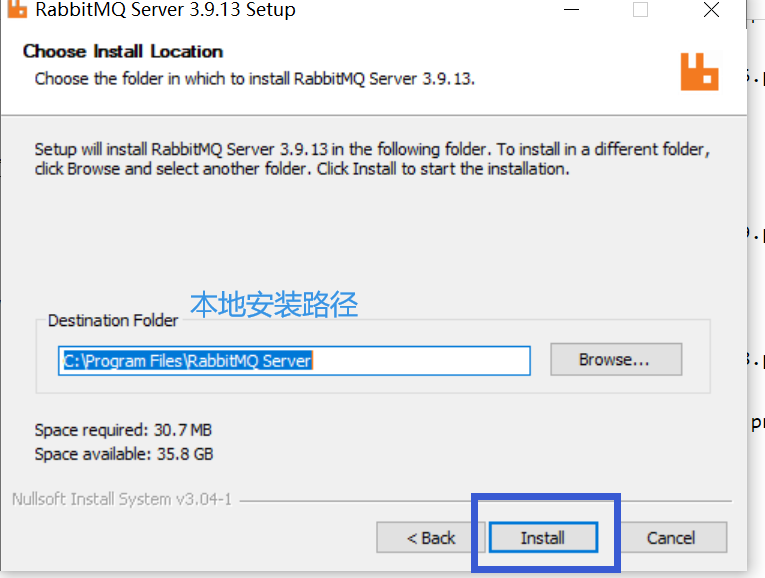
4、选择本地安装路径，点击Install，

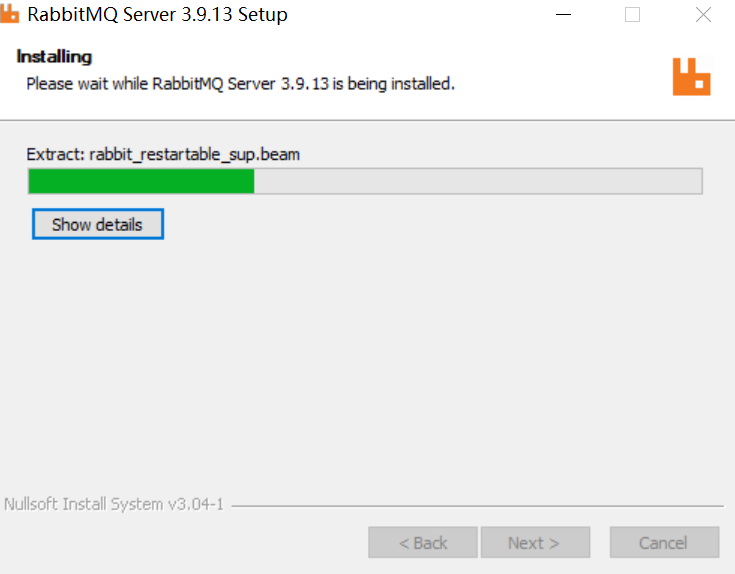
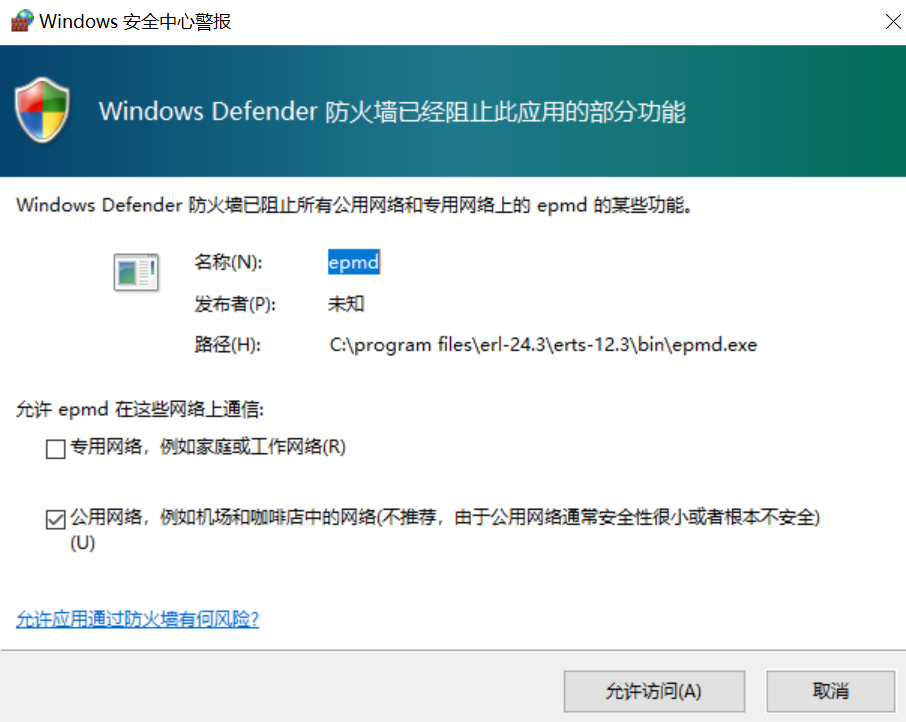
  • 弹出防火墙，选择允许访问



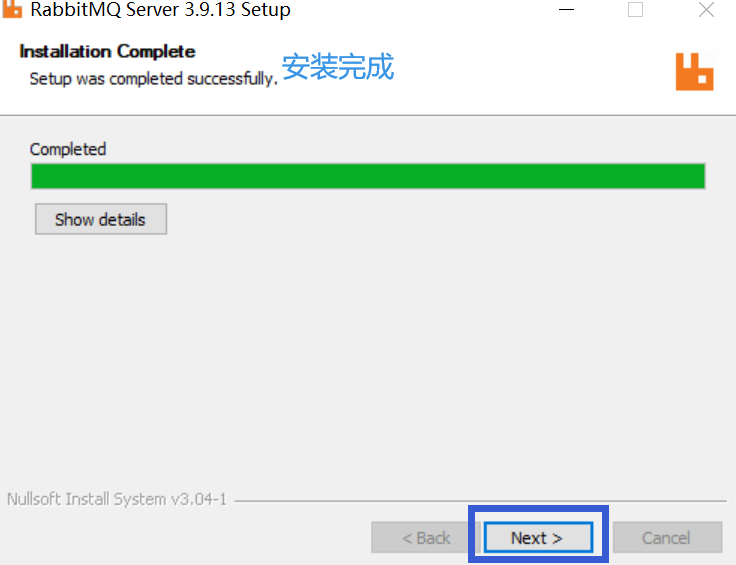
5、安装完成，点击next，点击finish结束。

三、RabbitMQ-Plugins安装（可视化管理插件）

1、找到RabbitMQ安装目录，windows+R打开命令行，输入cmd，打开命令界面，cd 到文件夹下。

2、输入如下命令进行安装。



rabbitmq-plugins enable rabbitmq_management

3、输入如下命令进行安装成功测试。



rabbitmqctl status

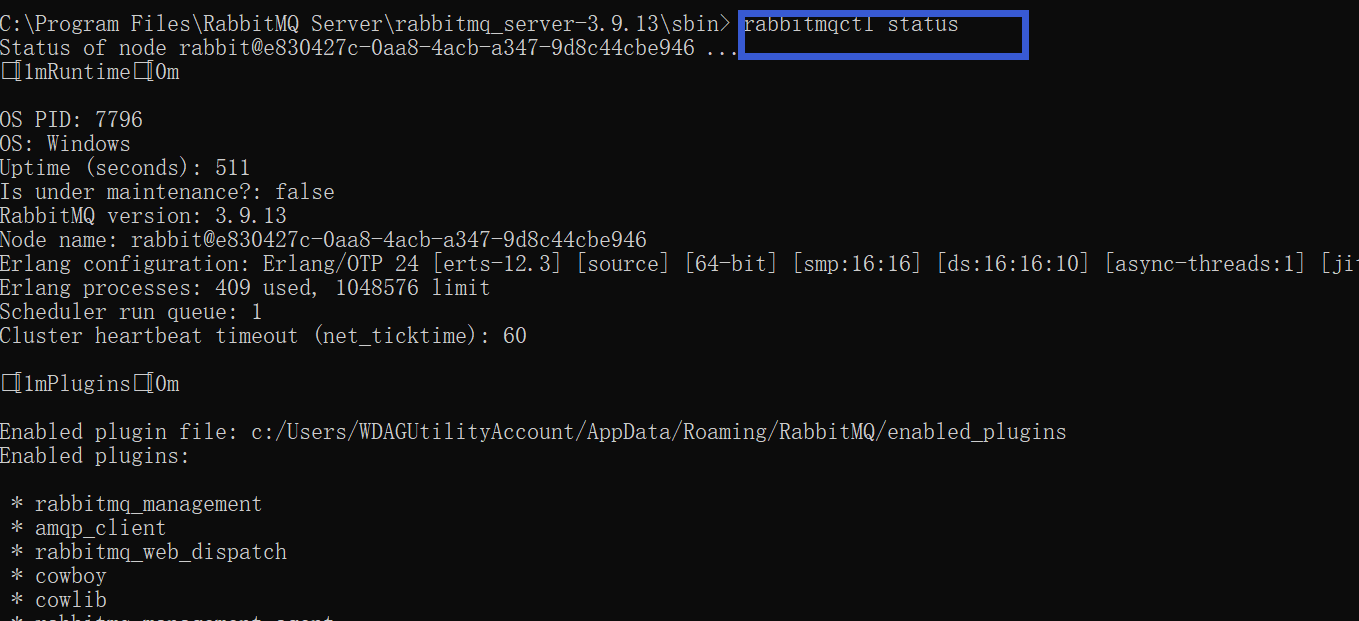
4、双击如图脚本进行启动。

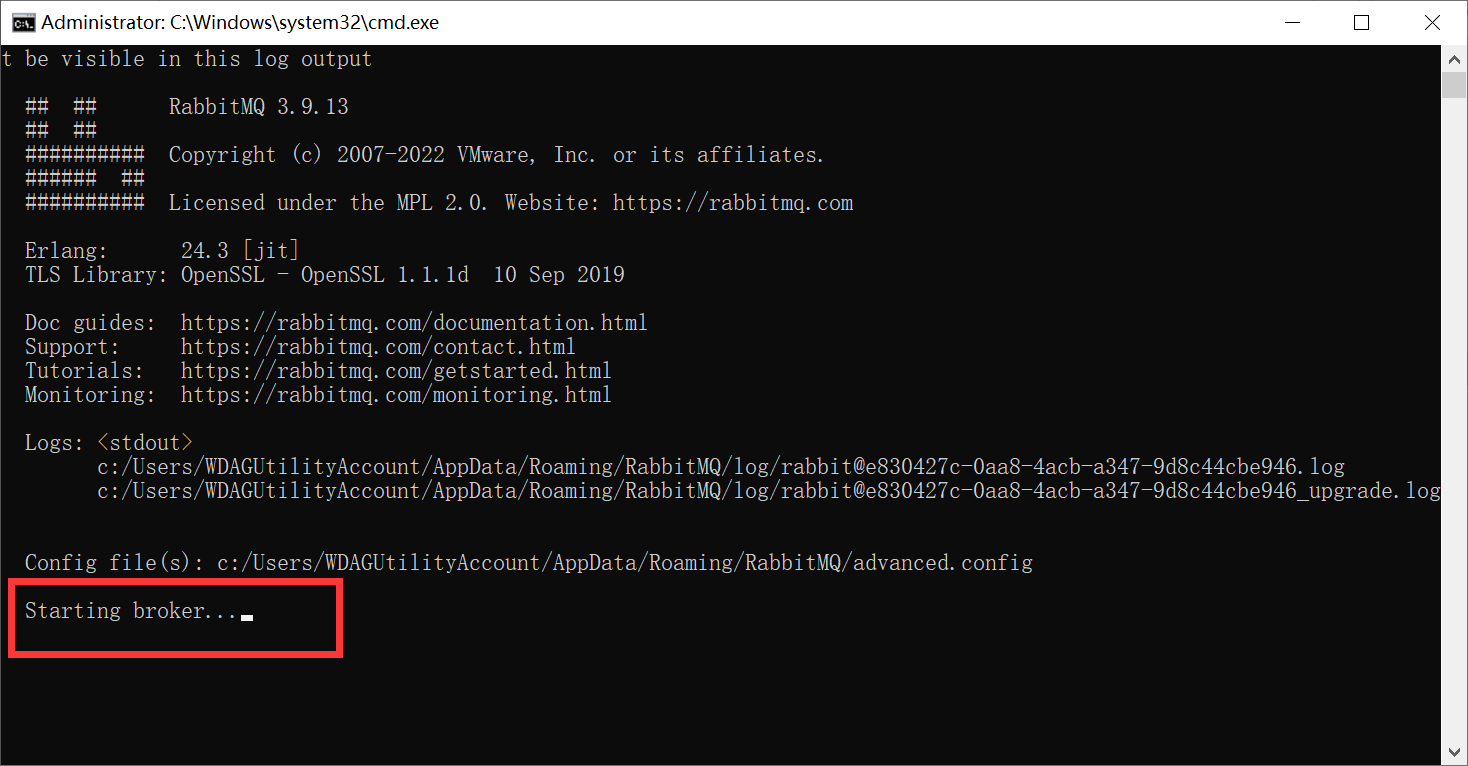
  • 出现闪退，找到如图的rabbitmq command prommpt双击打开

  • 在路径下，新建文件夹DATA

  • 执行命令，清楚服务



rabbitmq-service.bat remove

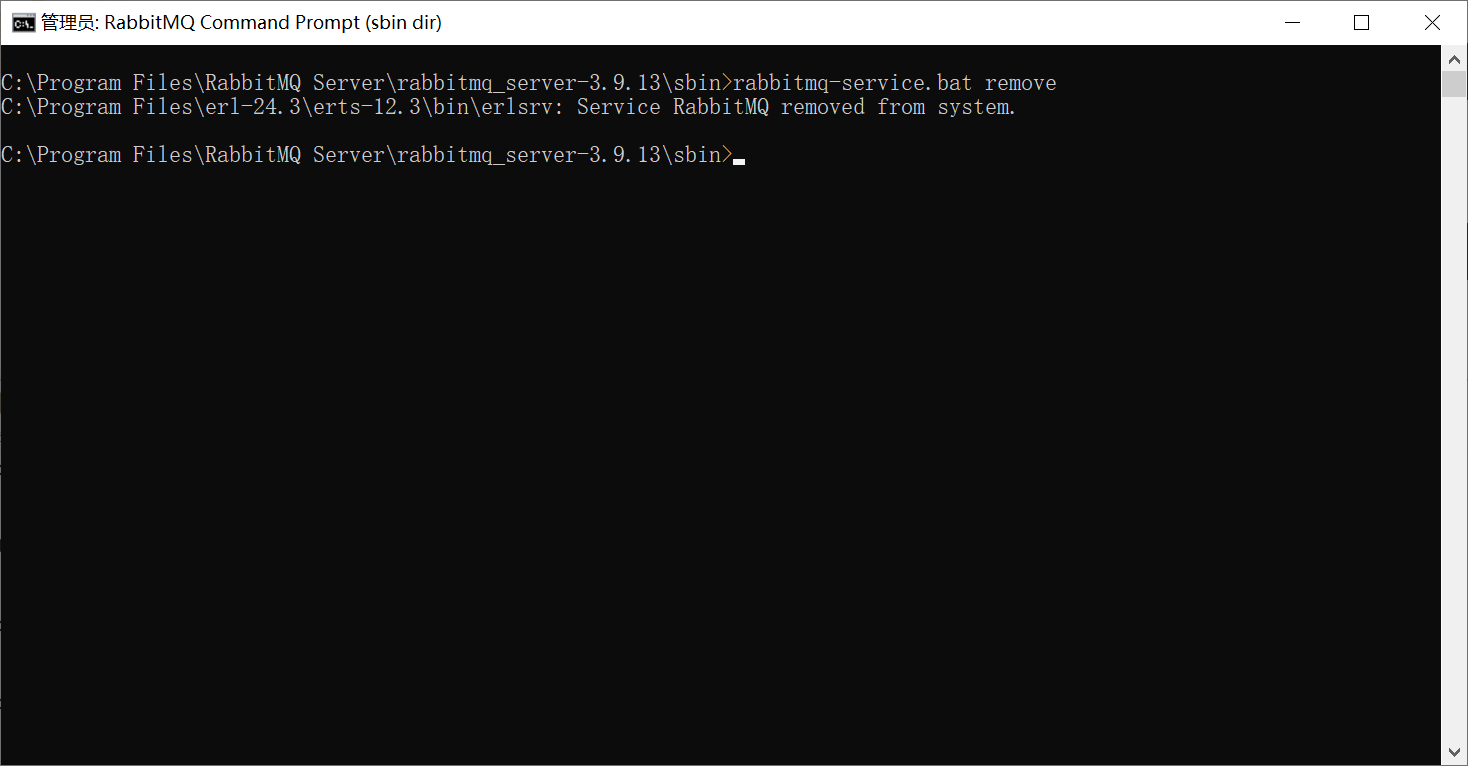
  • 设置数据路径。


set RABBITMQ_BASE=C:\Program Files\RabbitMQ Server\rabbitmq_server-3.9.13\DATA

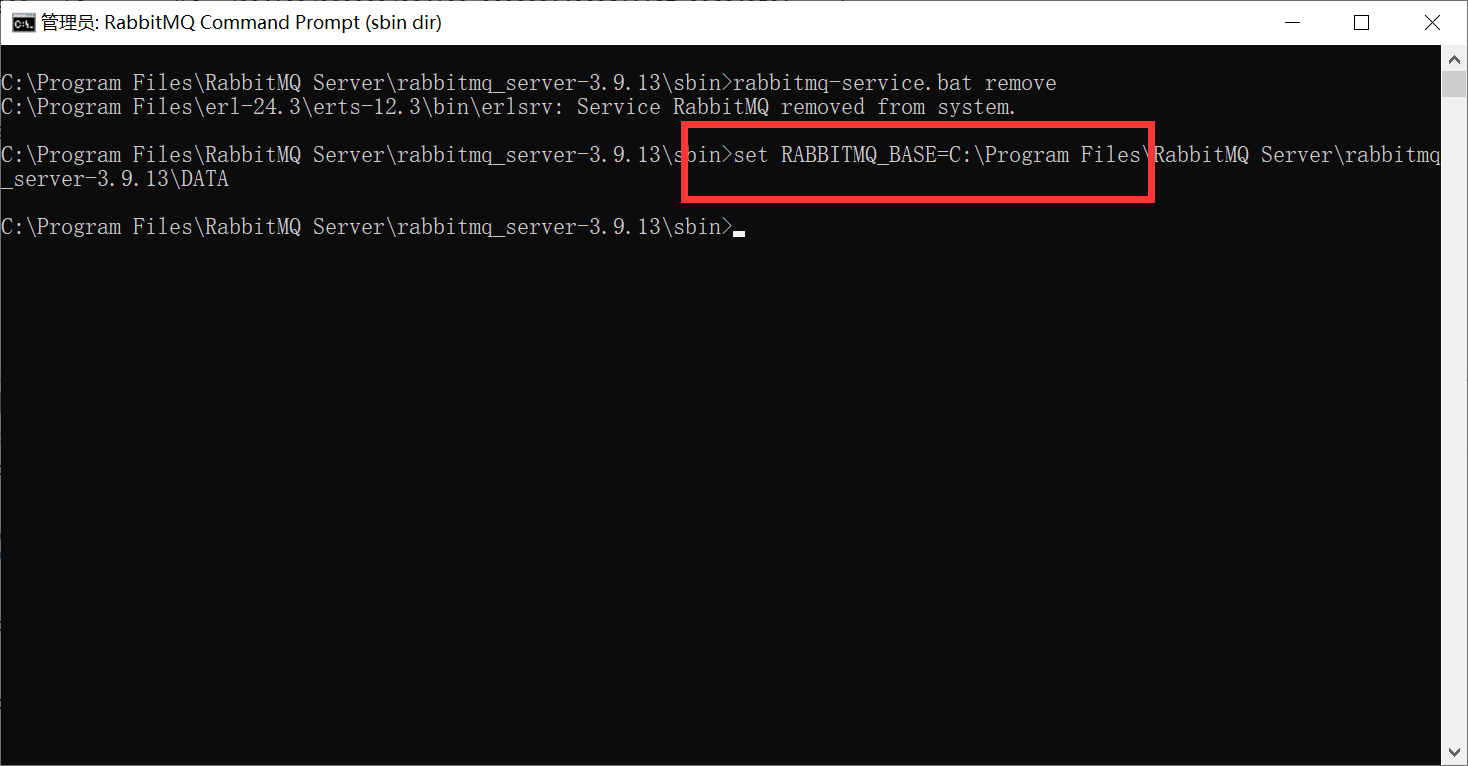
  • 重新加载服务


rabbitmq-service.bat install

  • 重新加载组件


rabbitmq-plugins enable rabbitmq_management

  • 开启服务（当前位置命令启动）


net start rabbitmq

  • 或者点击启动

5、输入网址到浏览器访问:http://localhost:15672/

6、输入用户名/密码:guest/guest 登录访问

2022年官网下安装RabbitMQ最全版与官网查阅方法的更多相关文章

  1. 2022年官网下安装Logstash最全版与官网查阅方法（8.1.0最新安装）

    一.环境整合 构建工具(参考工具部署方式) 软件名称 版本 相关文章推荐 NodeJS 16.0.0 https://www.cnblogs.com/liuyangfirst/p/15998172.h ...

  2. 2022年官网下安装MongoDB最全版与官网查阅方法（5.0.6）

    一.下载安装 1.百度搜索,找到官网,或直接访问:https://www.mongodb.com/ 2.寻找下载位置,双击下载. 3.找到本地位置,双击执行,进入欢迎界面,选择next. 4.勾选协议 ...

  3. 2022年官网下安装MAVEN最全版与官网查阅方法

    目录 确保JDK安装无误 一.百度输入关键字maven,选择官网,进入官网 二.找到下载位置,如图所示,双击进入 三.找到下载位置(下载的是安装包bin版本的,src是源码查看),双击下载 四.弹出保 ...

  4. 2022年官网下安装MySQL最全版与官网查阅方法

    目录 安装部署MySQL 一.百度查找MySQL官网 二.如图找到DOWNLOADS位置,既是下载位置 三.双击进入DOWNLOADS,下拉找到如图位置(红圈位置是社区免费版,上边部分应该是收费版) ...

  5. 2022年官网下安装DBever最全版与官网查阅方法

    目录 安装部署DBeaver 一.官网下载安装 1.百度搜索DBeaver. 2.进入主页,点击DownLoad下载. 3.查看列表,选择windows的exe版本下载. 4.找到位置,双击打开,弹出 ...

  6. 2022年官网下安装Redis最全版与官网查阅方法

    目录 安装部署Redis 一.下载安装 1.百度搜索Redis,双击进入. 2.下载稳定版(服务器版本),如图所示 3.找到下载的位置,解压压缩包(查看发现不是windows版本) 4.官网没有win ...

  7. 2022年官网下安装Elasticsearch最全版与官网查阅方法（8.1.0最新安装）

    目录 一.环境整合(需要提前装好) 构建工具(参考工具部署方式) 二.官方下载Elasticsearch部署安装 1.百度搜索"Elasticsearch",或者访问官网https ...

  8. 2022年官网下安装Kibana最全版与官网查阅方法（Kibana8.1.0+Elasticsearch8.1.0）

    一.环境整合(需要提前装好) 构建工具(参考工具部署方式) 软件名称 版本 相关文章推荐 Elasticsearch ..* https://www.cnblogs.com/liuyangfirst/ ...

  9. 2022年官网下安装GIT最全版与官网查阅方法

    目录 安装部署Git 1.百度搜索git,双击进入. 2.进入主页,双击如图位置. 3.进入下载列表,双击下载. 4.找到本地文件位置,双击安装,弹出界面,选择next 5.进入安装路径位置,修改路径 ...

随机推荐

  1. Git refusing to merge unrelated histories （拒绝合并不相关仓库）

    感谢原文作者:lindexi_gd 原文链接:https://blog.csdn.net/lindexi_gd/article/details/52554159 本文讲的是把git在最新2.9.2,合 ...

  2. Ubuntu安装 php + apache + mysql

    转载请注明来源:https://www.cnblogs.com/hookjc/ 1.安装SSH(必须) sudo apt-get install ssh 2.安装MySQL(虽然现在最新版为5.1,但 ...

  3. VC 为程序创建唯一标识

    转载请注明来源:https://www.cnblogs.com/hookjc/ 应用: 一台机器上只许运行一个客户端 同一个账号只允许登陆一个客户端 BOOl m_IsRun=false; HANDL ...

  4. Java数组3种创建方式

    public static void main(String[] args){ /** * 1. 固定大小的空数组, 动态创建 */ String[] strArr1 = new String[3]; ...

  5. 企业级Docker容器镜像仓库Harbor的搭建

    Harbor简述 Habor是由VMWare公司开源的容器镜像仓库.事实上,Habor是在Docker Registry上进行了相应的企业级扩展,从而获得了更加广泛的应用,这些新的企业级特性包括:管理 ...

  6. rtsp监控直播转码用到EasyNVR

    第一 下载EasyNVR_win_v2.6.18.0320 第二 安装启动 第三 配置转码路径 http://localhost:10800/ 最后转码播放 /hls/stream_1/stream_ ...

  7. Docker之LNMP分布式容器部署

    Docker之LNMP分布式容器部署 目录 Docker之LNMP分布式容器部署 一.项目模拟 1. 项目环境 2. 服务器环境 3. 任务需求 二.Linux系统基础镜像 三.Nginx 1. 建立 ...

  8. 任意文件上传漏洞syr

    任意文件上传漏洞 先来几个一句话木马看看 <%execute(request("value"))%> #asp木马 <?php eval($_POST[" ...

  9. postman常用测试脚本

    测试脚本: 设置环境变量 var jsonData = JSON.parse(responseBody); postman.setGlobalVariable("5KMST", j ...

  10. PHP面试常考内容之面向对象（3）

    PHP面试专栏正式起更,每周一.三.五更新,提供最好最优质的PHP面试内容.继上一篇"PHP面试常考内容之面向对象(2)"发表后,今天更新面向对象的最后一篇(3).需要(1),(2 ...