Code Forces 711D Directed Roads

D. Directed Roads

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from 1to n.

There are n directed roads in the Udayland. i-th of them goes from town i to some other town ai (ai ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.

ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak (k > 1) such that for every 1 ≤ i < k there is a road from town Ai to town Ai + 1 and another road from town Ak to town A1. In other words, the roads are confusing if some of them form a directed cycle of some towns.

Now ZS the Coder wonders how many sets of roads (there are 2n variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.

Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.

Input

The first line of the input contains single integer n (2 ≤ n ≤ 2·105) — the number of towns in Udayland.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes a road going from town i to town ai.

Output

Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.

Examples

input

3
2 3 1

output

6

input

4
2 1 1 1

output

8

input

5
2 4 2 5 3

output

28

Note

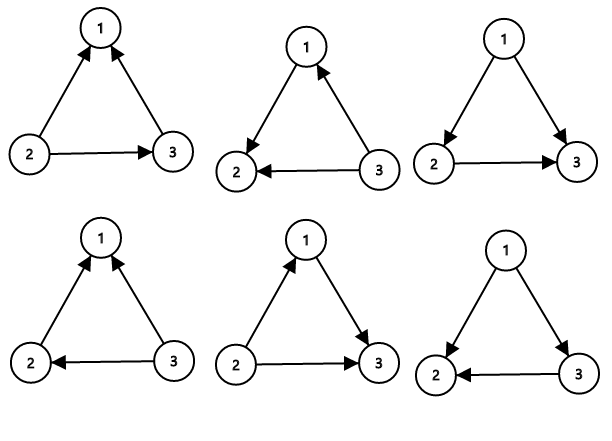
Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are , ,  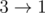initially. Number the roads 1 to 3 in this order.

The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.

The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.

题意：给定N个城市，给定N条有向边，然后你可以对任意条边进行翻转(改变方向),求出所有翻转后不含有环的图的个数？

题解：首先假设原给的图中不含有环，那么方法数就是2^N。如果原图中存在环，那么对一个环进行怎样的操作可以把环消掉呢？假设环由x条边组成，那你会发现除了2种操作会继续保持环外:

对环内的边什么都不操作，对环内的所有边全部翻转。那么结果就很明显了，破坏一个环的方法数就是（2^x-2）。所以问题就转化成为找到原图中所有的环，以及每个环的边数。

代码如下：

#include <iostream>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <map>
#include <set>
#include <bitset>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <string>
#include <sstream>
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
#define mod 1000000007
#define mt(A,B) memset(A,B,sizeof(A))
using namespace std;
typedef long long LL;
const int N=200000+10;
const LL INF=0x3f3f3f3f3f3f3f3fLL;
LL to[N],vis[N],pre[N],ans=1,dis[N],T=0,sum=0;
void init()
{
    pre[0]=1;
    mt(vis,0);mt(dis,0);
    for(int i=1;i<=N;i++)pre[i]=(pre[i-1]*2)%mod;//预处理2^i
}
void dfs(int x,int cur)//找环
{
    vis[x]=T;//T代表的是第几次的dfs,
    dis[x]=cur;//dis[x]代表第T次的dfs从起点走到x用了多少步
    if(vis[to[x]])
    {
       if(vis[to[x]]==vis[x])//如果to[x]被访问且，dfs序相同，那么说明有环
       {
            int num=dis[x]-dis[to[x]]+1;
            sum+=num;
            ans=ans*(pre[num]-2+mod)%mod;
       }
    }
    else dfs(to[x],cur+1);
}
int main()
{
#ifdef Local
    freopen("data.txt","r",stdin);
#endif
    int i,j,k,n;
    cin>>n;
    init();
    for(i=1;i<=n;i++)
    {
        scanf("%I64d",&to[i]);
    }
    for(i=1;i<=n;i++)
    {
        if(!vis[i])
        {
            T++;
            dfs(i,1);
        }
    }
    ans=ans*(pre[n-sum])%mod;
    cout<<ans<<endl;
}