Bellman-Bord（贝尔曼-福特）

include

const int inf=0x3f3f3f3f;
int main()
{
int m,n;
scanf("%d%d",&n,&m);
int u[n+1],v[n+1],w[n+1];
for(int i=1; i<=m; i++)
scanf("%d%d%d",&u[i],&v[i],&w[i]);
int dis[n+1];
for(int i=1; i<=n; i++)
dis[i]=inf;
dis[1]=0;
for(int k=1; k<=n-1; k++)
{

    for(int i=1; i<=m; i++)
        if(dis[v[i]]>dis[u[i]]+w[i])
            dis[v[i]]=dis[u[i]]+w[i];

}
int check=0;
for(int i=1;i<=m;i++)
    if(dis[v[i]]>dis[u[i]]+w[i])check=1;//进行第n次松弛
if(check==1)printf("有回路");
else
{
    for(int i=1;i<=n;i++)
        printf("%d\n",dis[i]);
}
return 0;

}

图解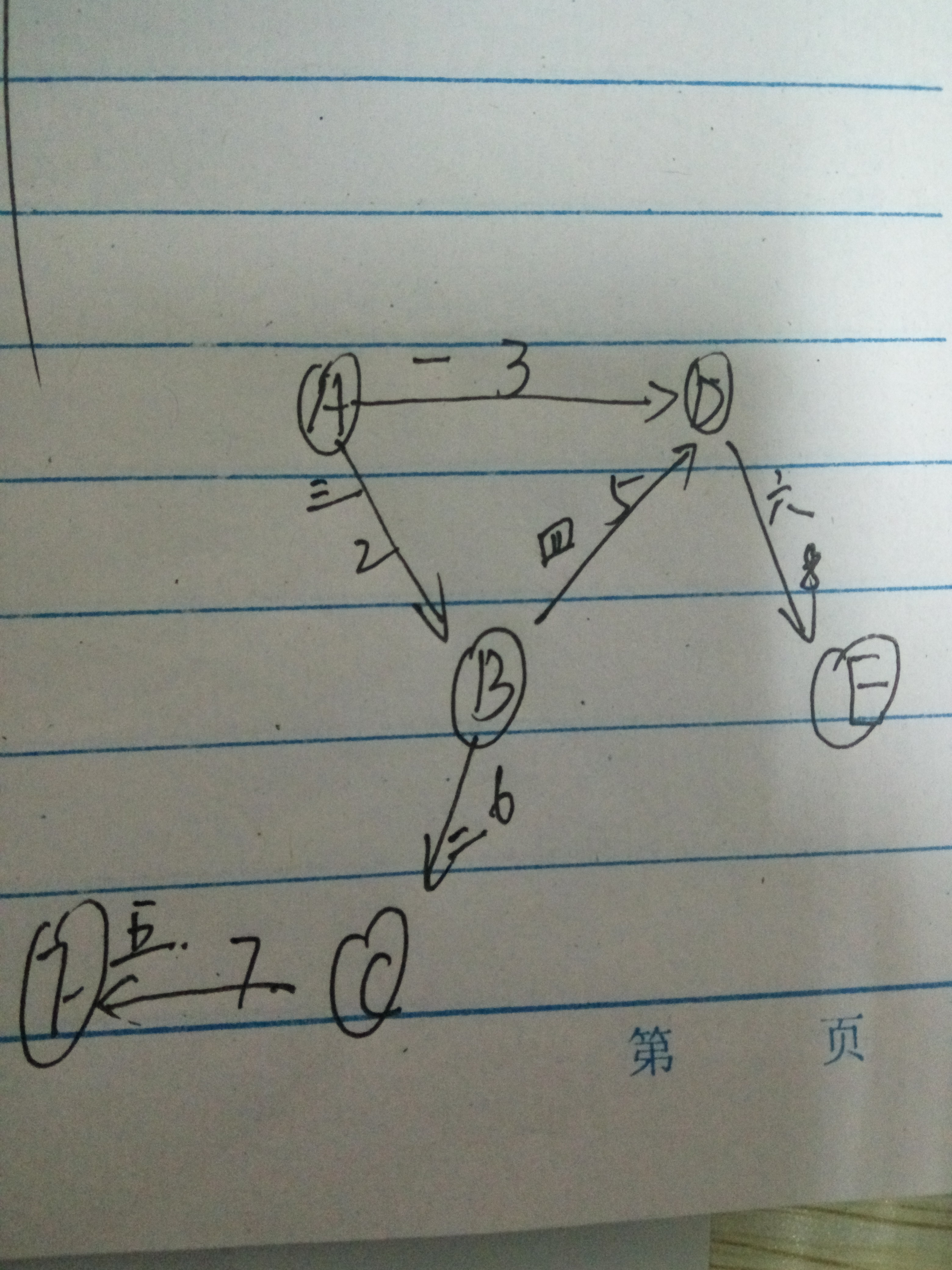

A是源点
1： 初始化 A到所有的点都是 无穷大 dao自身的距离为0；
2： 开始遍历第一条边 A--->D 即以A作为中转站 A---->A--->D A到A的距离为0 A到D的距离为3 所以A到D的距离从无穷大变为3
3： 遍历第二条边 B----->C 以B作为中转站 A---->B---->C 此时A到B的距离为无穷大 B到C的距离为6 所以A到C的距离为无穷大 松弛失败
4： 遍历第三条边 A---->B 以A作为中转站 A---->A--->B A到A的距离为0 A到B的距离为2 所以A到B的距离从无穷大变为2
5： 遍历第四条边B----->D 以B作为中转站 A---->B---->D A到B的距离为2 B到D的距离为5 但是又第二步已经计算出D到源点的距离为3且
小于5+2 即A到D的距离不变还是原来的3
6： 遍历第五条边 C---->F 以C作为中专站 A---->C---->F A到C的距离为无穷大 C到F的距离为7 所以A到F的距离为无穷大 即松弛失败
7：遍历第六条边 D---->E 以D作为中专站 A---->D---->E A到D的距离为3 D到E的距离为8 所以A到E的距离为8+3=11

经过一轮松弛之后发现还存在点到源点的距离是无穷大的 显然不合理
因为在执行第三步时 由于B到A的距离为无穷大 所以不能经B中转使得C到A的距离变短 但是 在执行第四步时 B到A的距离就已经变为2了
明显可以用B来作为中转站使得C到A的距离变短 由此可见 还需进行一轮松弛

那么之多进行多少轮松弛呢 应该是n-1(顶点的个数减一，这是最坏的情况 即是每轮只松弛了一条边)
如果进行第n松弛仍可以是最短路发生变化，说明此图中存在负全回路

当然这种可能性不大 大多数情况下松弛不到n-1轮就已经是最短了 再继续进行松弛时也不会发生变化

所以可以优化 （SPFA）