Uva_11722 Joining with Friend

题目链接

题意：

　　两个人坐火车， 在某个城市到站的时间段分别为[t1, t2] , [s1, s2]，停在站台的时间均为w。

　　问， 若两人能见面的概率。

思路：

　　一道基础的几何概型， p = s(m)/s(n)。

　　令x1 = t1, x2 = t2。

　　令y1 = s1, y2 = s2。

　　这样这四条直线就围成一个矩形，若两人见面， 则应该满足在 y = x ± w 这两条直线之间。

　　即本题求解， y = x ± w 在矩形中所围面积 与矩形面积之比。

　　根据 y = x + b 这条线与矩形的交点不同， 把矩形分成四个区域， 计算面积这里规定以左上角的点为参考点计算。

　　阴影面积即为所求

　　1）

　　

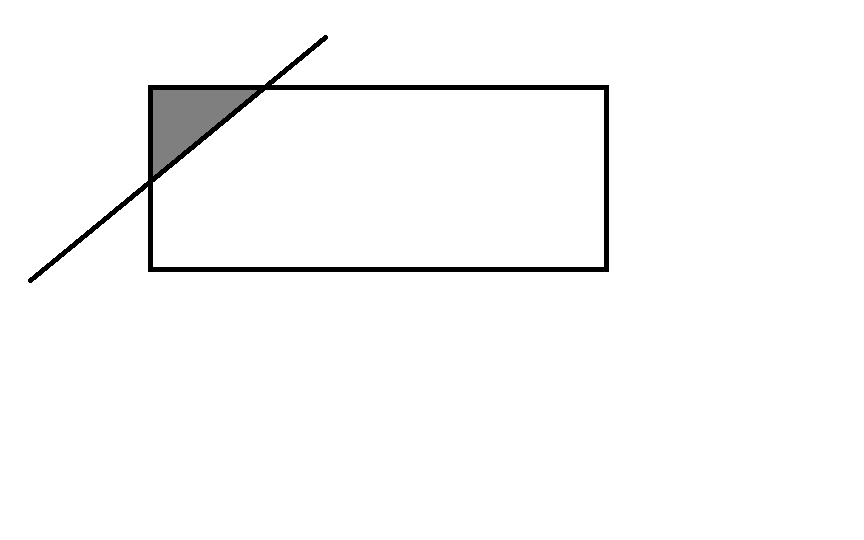
　　2）

　　这种情况将之补成一个三角形， 用大三角形减去小三角形的面积即可。

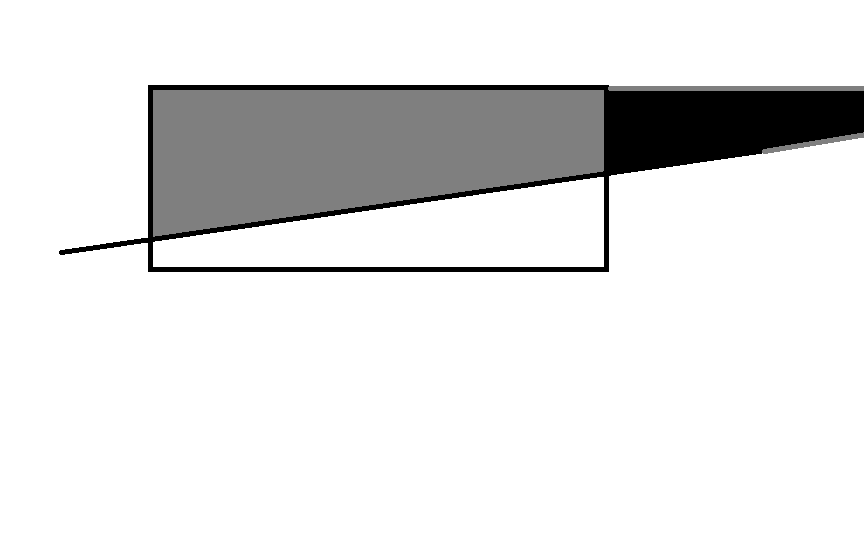
　　3）

　　这种情况， 用矩形面积减去小三角形面积即可。

　　4）

　　这种情况也用补全三角形来求解

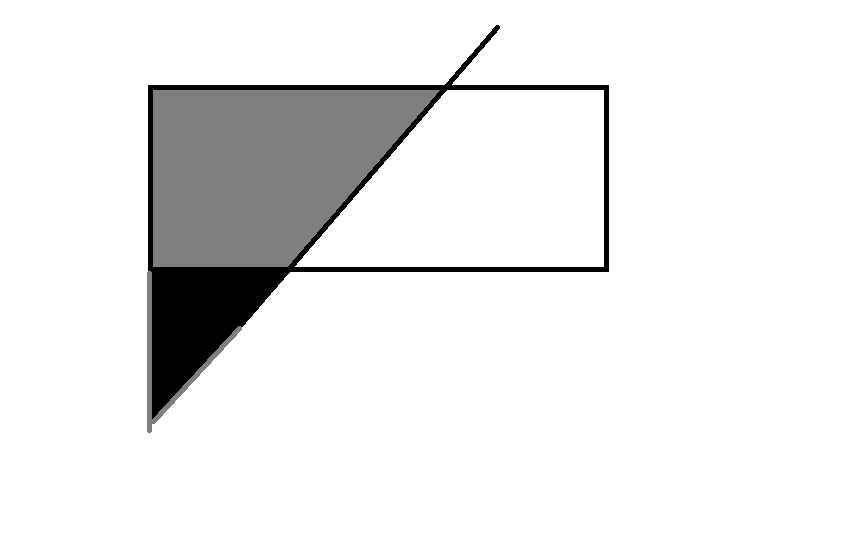
　　other)

　　如果直线相交于左上角， 那么面积为0. 如果在右下角， 那么面积为矩形面积。

　　

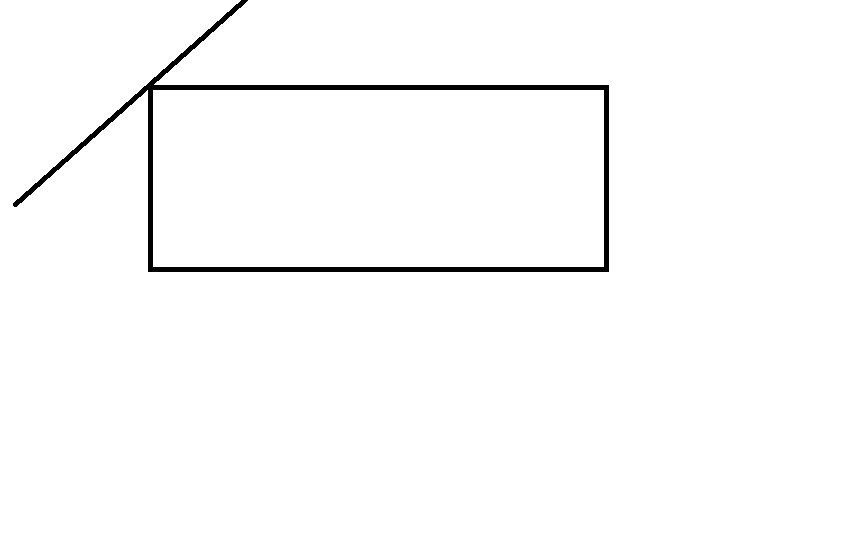
代码如下：

 #include <cmath>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <ctime>
 #include <climits>
 #include <set>
 #include <map>
 #include <list>
 #include <queue>
 #include <string>
 #include <vector>
 #include <fstream>
 #include <iterator>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 #define LL long long
 #define MAXN 4
 #define MOD 1000000007
 #define eps 1e-6
 double s[MAXN], t[MAXN], w;
 double weight, high;
 double get_area(double b)
 {
     double tx = t[] - b;
     double dx = t[] - b;
     double ly = s[] + b;
     double ry = s[] + b;
     //printf("tx: %.7lf, dx: %.7lf, ly: %.7lf, ry: %.7lf\n", tx, dx, ly, ry);
     bool OnTop = (tx <= s[] && tx >= s[]);
     bool OnDown = (dx <= s[] && dx >= s[]);
     bool OnLeft = (ly <= t[] && ly >= t[]);
     bool OnRight = (ry <= t[] && ry >= t[]);

     if(OnTop && OnLeft)
         return 0.5 * (tx - s[]) * (t[] - ly);
     if(OnLeft && OnRight)
         return 0.5 * ((t[] - ly) * (tx - s[]) - (t[] - ry) * (tx - s[]));
     if(OnDown && OnTop)
         return 0.5 * ((tx - s[]) * (t[] - ly) - (dx - s[]) * (t[] - ly));
     if(OnDown && OnRight)
         return weight * high - 0.5 * (s[] - dx) * (ry - t[]);
     return ly >= t[] ?  : weight * high;
 }

 int main()
 {
     int T;
     int kcase = ;
     scanf("%d", &T);
     while(T --)
     {
         scanf("%lf %lf %lf %lf %lf", &t[], &t[], &s[], &s[], &w);
         high = t[] - t[];
         weight = s[] - s[];
         double area_top = get_area(w);
         double area_down = get_area(- * w);
         double ans = high * weight;
         //printf("%.8lf %.8lf %.8lf\n", area_top, area_down, ans);
         ans = (area_down - area_top) / ans;
         printf("Case #%d: %.8lf\n", ++ kcase, ans);
     }
     return ;
 }