Codeforces 595D - Max and Bike

595D - Max and Bike

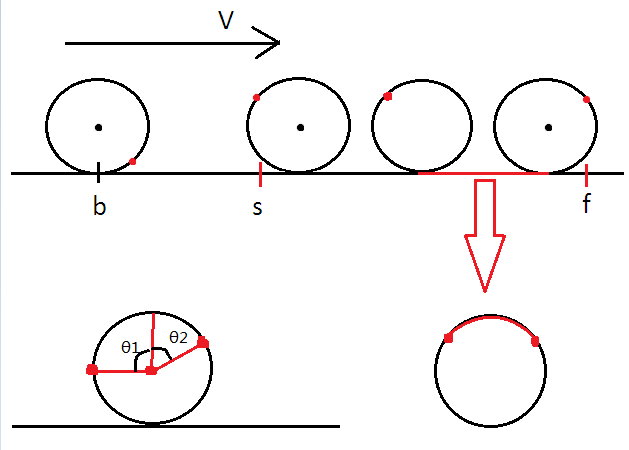
思路：开始和结束时的计时器的高度相同时（也就是关于圆竖着直径对称）时间最少。

证明：

总距离为d.

圆周长为s=2*π*r.

设len=d-floor(d/s）*s.

len=θ₁*r+θ₂*r+sin(θ₁)*r+sin(θ₂)*r.

要使sin(θ₁)*r+sin(θ₂)*r尽可能大，或者说θ₁*r+θ₂*r尽可能小。

根据和差化积公式的

sin(θ₁)+sin(θ₂)=2*sin((θ₁+θ₂)/2)*cos((θ₁-θ₂)/2)

(θ₁-θ₂)越趋近与0，值越大。

所以θ₁=θ₂=θ

所以变量只剩下一个变量θ了，而且函数是单调的，所以二分解三角函数。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define mp make_pair
#define pi acos(-1.0)
#define pii pair<int,int>
#define mem(a,b) memset(a,b,sizeof(a))
#define MAX(a,b,c) max(a,max(b,c)) 

const int INF=0x7f7f7f7f;
const int MOD=1e9+;
const double eps=1e-;

int main()
{
    /*ios::sync_with_stdio(false);
    cin.tie(0);*/
    int n,r,v;
    scanf("%d%d%d",&n,&r,&v);
    double s=pi*r*;
    while(n--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        double d=b-a;
        int c=(d/s);
        double len=d-c*s;
        double L=,R=len;
        double mid=(L+R)/;
        while(R-L>=eps)
        {
            if(mid+*r*sin(mid//r)>=len)R=mid;
            else L=mid;
            mid=(L+R)/;
        }
        printf("%.12lf\n",(c*s+mid)/v);
    }
    return ;
}