[数学] 将长为L的木棒随机折成3段，则3段构成三角形的概率

1.题目

　　如题，将长为L的木棒随机折成3段，则3段构成三角形的概率是多少？

2.解析

　　这个与其说是编程题目，倒不如说是个数学题目。可能是你没有见过，或者没有过这种解题思想。（还是那句，一回生两回熟，类推吧）

　　设分成的三段木棍的长度分别为：x，y，L-x-y。

　　(1)首先，三边长度都大于0。可以有下面的推导公式：

　　

　　　可以知道，满足条件的区域面积为，(1/2)*L*L，如下所示（就是阴影区域的面积大小）：

　　　

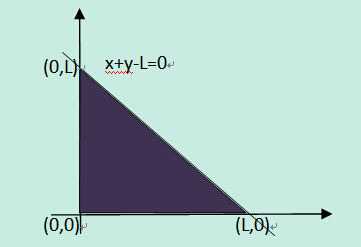
　　(2)其次，要构成三角形，必须满足任意两边之和大于第三边(也就是任意两边之差小于第三边)。可以有下面的推导公式：

　　

　　可以知道，满足条件的区域面积为，(1/8)*L*L，如下所示（就是阴影区域的面积大小）：

　　

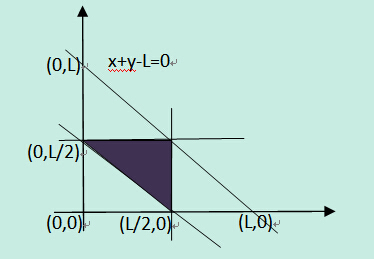
　　从上面的分析可知，任意分成三段，按照三段的长度来讲。能组成三角形的情况占所有分割情况的1/4。

　　所以，将长为L的木棒随机折成3段，则3段构成三角形的概率为0.25。