题解 P1801 【黑匣子_NOI导刊2010提高（06）】

蒟蒻来发题解了。我仔细看了一下其他题解，各位巨佬用了堆，红黑树，splay,treap之类的强大算法，表示蒟蒻的我只会口胡这些算法，所以我决定用一种极其易理解的算法————fhq treap，作为treap的升级版，它不仅好理解，好用，还能做到可持久化，真是神级算法（不知道为什么会fhq treap的我，不会一般treap）

进入正题，首先我先讲讲fhq treap的主要思想，它是一种非旋转的平衡树，不用考虑左旋右旋等麻烦情况，它很暴力，直接靠拆树，合并来实现，有点二分的感觉，其实它很多操作就有二分思想。

好了，看图，我们有一颗二叉树

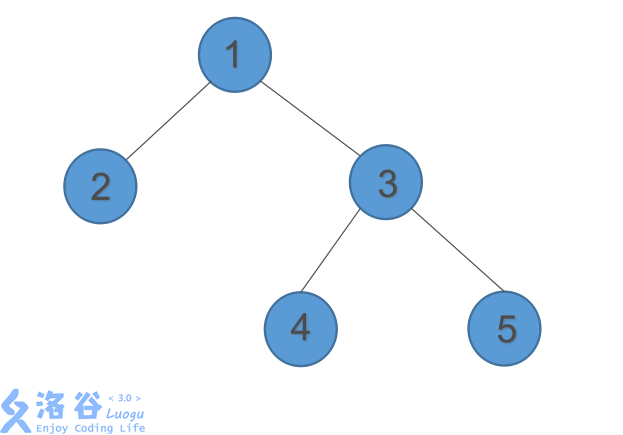
当我们插入6号，发现它失衡了

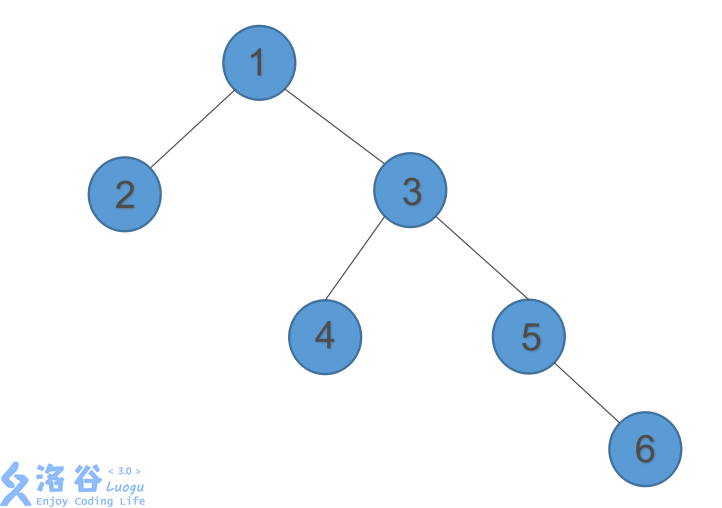
多西太？大丈夫

我们不用旋转，不用交换，直接拆。

第一个重要操作：拆树（split），我们先把树分为x,y两部分，x的节点权值≤k， y的节点的权值＞k，要插入一个数a的话，就把新的节点a看做是一棵树，先与x合并，合并完之后将合并的整体与y合并

上代码

 inline void split(int &x,int &y,int k,int pos)
 {
     if(!pos)x=y=;//root=0时（即第一次split） 此时的x=?,y=?很明显要给他们初始化 即x=0,y=0
     else
     {
         if(val[pos]<=k)
         {x=pos;split(son[pos][],y,k,son[pos][]);}
         else
         {y=pos;split(x,son[pos][],k,son[pos][]);}
         update(pos);
     }
 }

第二个重要操作：合并（merge） 还是两棵树x,y。如果rand[x]<rand[y] 我们就把y接在x的右儿子上 你想如果接在左儿子 那左儿子的权值就大于父亲的权值了 不符合二叉搜索树的性质

反之同理

其实merge 要理解的话自己画两颗treap 然后模拟一下。

上代码

 inline int merge(int x,int y)
 {
     if(x==||y==) return x+y;//第一次合并的情况
     if(rnd[x]<rnd[y])
     {
         son[x][]=merge(son[x][],y);
         update(x);return x;
     }
     else
     {
         son[y][]=merge(x,son[y][]);
         update(y);return y;
     }
 }

至于查排名（find），就是easy的操作了，根据堆的性质，直接找右子树大小，再去遍历就好了，不知道的可以先去学习二叉搜索树的操作（各位巨佬肯定都会了）

ac代码

 #include<iostream>
 #include<cstdio>
 #include<ctime>
 #include<cstdlib>
 #include<cstring>
 #include<algorithm>
 #define maxn 200010
 using namespace std;
 int n,val[maxn],rnd[maxn],son[maxn][],size[maxn],sum_p,m;
 //val记录权值，son记录左右子树大小，size[i]记录以i为根节点的树的大小
 int X1[maxn];
 int flag[maxn];
 inline void read(int &x)//快读
 {
     x=;int f=;
     char ch=getchar();
     while(ch<''||ch>'')
     {if(ch=='-') f=-; ch=getchar();}
     while(ch>=''&&ch<='')
     {x=x*+ch-'';ch=getchar();}
     x*=f;
 }
 inline int newnode(int x)
 {
     ++sum_p;size[sum_p]=;
     val[sum_p]=x;rnd[sum_p]=rand();
     return sum_p;
 }
 inline void update(int x)
 {
     size[x]=size[son[x][]]+size[son[x][]]+;//加上自己
 }
 inline void split(int &x,int &y,int k,int pos)//x,左子树的根(权值较小的),y,右子树的根,pos为现在的节点
 {
     if(!pos)x=y=;//root=0时（即第一次split） 此时的x=?,y=?所以初始化x=0,y=0
     else
     {
         if(val[pos]<=k)
         {x=pos;split(son[pos][],y,k,son[pos][]);}
         else
         {y=pos;split(x,son[pos][],k,son[pos][]);}
         update(pos);
     }
 }
 inline int merge(int x,int y)//保证y子树权值大于x子树
 {
     if(x==||y==) return x+y;//第一次合并的情况
     if(rnd[x]<rnd[y]) //比rand大小
     {
         son[x][]=merge(son[x][],y);
         update(x);return x;
     }
     else
     {
         son[y][]=merge(x,son[y][]);
         update(y);return y;
     }
 }
 inline int find(int pos,int rank)
 {
     while()
     {
         if(size[son[pos][]]>=rank)
         {
             pos=son[pos][];
         }
         else
         if(size[son[pos][]]+==rank)return pos;//由于是儿子 要加上自己
         else
         {
             rank-=size[son[pos][]]+;
             pos=son[pos][];
         }
     }
 }
 int main()
 {
     srand((unsigned)time(NULL));
     int a,b,x,y,z,op,root=,pos=;
     read(n),read(m);
     for(register int i=;i<=n;i++)
     read(X1[i]);
     for(register int i=;i<=m;i++)
     {read(op);flag[op]++;}//记录查询点
     for(register int i=;i<=n;i++)
     {
         split(x,y,X1[i],root);
         root=merge(merge(x,newnode(X1[i])),y);
         while(flag[i]>=)//可能一个位置不止一次查询
         {
             pos++;flag[i]--;
             printf("%d\n",val[find(root,pos)]);
         }
     }
 }

最后我再给没学过fhq treap的同学补充一点基础操作

1、求a的排名：我们只需要split成一颗≤a-1,一颗≥a的就行了 a的排名就是第一棵treap的size+1；

2、求a前驱：以a-1为界限拆树就好了，a的前驱肯定就是第一个treap里最大的 ，就在find操作的基础上，在x里找排名为size[x]的

3、求a后继：以a为界限拆树，a的后继是第二个treap里最小的；

4、delete和区间反转就留给大家自己思考了，无论如何，fhq treap的操作基本上都建立在拆树与合并上。

最后强烈安利一波fhq treap