Caffe源码阅读(1) 全连接层

发表于 2014-09-15 |

今天看全连接层的实现。
主要看的是https://github.com/BVLC/caffe/blob/master/src/caffe/layers/inner_product_layer.cpp

主要是三个方法，setup，forward，backward

setup 初始化网络参数，包括了w和b
forward 前向传播的实现
backward 后向传播的实现

setup

主体的思路，作者的注释给的很清晰。
主要是要弄清楚一些变量对应的含义

1
2
3

M_ 表示的样本数
K_ 表示单个样本的特征长度
N_ 表示输出神经元的个数

为了打字方便，以下省略下划线，缩写为M，K，N

forward

实现的功能就是 y=wx+b

x为输入，维度 MxK
y为输出，维度 Nx1
w为权重，维度 NxK
b为偏置，维度 Nx1

具体到代码实现，用的是这个函数caffe_cpu_gemm，具体的函数头为

void caffe_cpu_gemm<float>(const CBLAS_TRANSPOSE TransA,
    const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K,
    const float alpha, const float* A, const float* B, const float beta,
    float* C)

略长，整理它的功能其实很直观，即C←αA×B+βC

const CBLAS_TRANSPOSE TransA  # A是否转置
const CBLAS_TRANSPOSE TransB  # B是否转置

# 这部分都比较直观不用解释了
const int M          
const int N
const int K
const float alpha
const float* A
const float* B
const float beta,
float* C

# 其中A维度是MxK，B维度是KxN，C维度为MxN

从实际代码来算，全连接层的forward包括了两步:

# 这一步表示 y←wx，或者说是y←xw'
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, (Dtype)1.,
      bottom_data, weight, (Dtype)0., top_data);
# 这一步表示 y←y+b
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, N_, 1, (Dtype)1.,
        bias_multiplier_.cpu_data(),
        this->blobs_[1]->cpu_data(), (Dtype)1., top_data);
# 所以两步连起来就等价于y=wx+b

backward

分成三步：

更新w
更新b
计算delta

用公式来说是下面三条：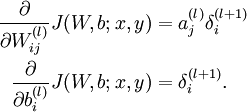

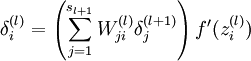
一步步来，先来第一步，更新w，对应代码是：

1 2	caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, (Dtype)1., top_diff, bottom_data, (Dtype)0., this->blobs_[0]->mutable_cpu_diff());

对照公式，有

1
2
3

需要更新的w的梯度的维度是NxK
公式中的a^(l)_j对应的是bottom_data，维度是KxM
公式中的\delta_(l+1)_i对应的是top_diff，维度是NxM

然后是第二步，更新b，对应代码是：

1
2
3

caffe_cpu_gemv<Dtype>(CblasTrans, M_, N_, (Dtype)1., top_diff,
        bias_multiplier_.cpu_data(), (Dtype)0.,
        this->blobs_[1]->mutable_cpu_diff());

这里用到了caffe_cpu_gemv，简单来说跟上面的caffe_cpu_gemm类似，不过前者是计算矩阵和向量之间的乘法的（从英文命名可以分辨，v for vector, m for matrix）。函数头：

void caffe_cpu_gemv<float>(const CBLAS_TRANSPOSE TransA, const int M,
    const int N, const float alpha, const float* A, const float* x,
    const float beta, float* y) 

# 实现的功能类似 Y←αAX + βY
# 其中A的维度为 MxN
# X是一个向量，维度为 Nx1
# Y是结果 ，也是一个向量，维度为Mx1

const CBLAS_TRANSPOSE TransA  # 是否对A进行转置

# 下面的参数很直观，不描述了
const int M
const int N
const float alpha
const float* A
const float* x
const float beta
float* y

绕回到具体的代码实现。。如何更新b？根据公式b的梯度直接就是delta

# 所以对应的代码其实就是将top_diff转置后就可以了（忽略乘上bias_multiplier这步）
caffe_cpu_gemv<Dtype>(CblasTrans, M_, N_, (Dtype)1., top_diff,
        bias_multiplier_.cpu_data(), (Dtype)0.,
        this->blobs_[1]->mutable_cpu_diff());

第三步是计算delta，对应公式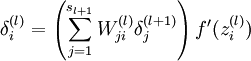

这里面可以忽略掉最后一项f’,因为在caffe实现中，这是由Relu layer来实现的，这里只需要实现括号里面的累加就好了，这个累加其实可以等价于矩阵乘法

caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, (Dtype)1.,
        top_diff, this->blobs_[0]->cpu_data(), (Dtype)0.,
        (*bottom)[0]->mutable_cpu_diff());

# top_diff为\delta^(l+1)_j 维度 MxN
# this->blobs_[0]->cpu_data()为W^(l)_ji 维度 NxK
# (*bottom)[0]->mutable_cpu_diff()是要计算的结果，也就是\delta^(l)_i 维度是MxK

附录

又及，这里具体计算矩阵相乘用的是blas的功能，描述页面我参考的是：https://developer.apple.com/library/mac/documentation/Accelerate/Reference/BLAS_Ref/Reference/reference.html#//apple_ref/c/func/cblas_sgemm