SciTech-Mathmatics - Advanced Linear Algebra: 矩阵乘法 的 四种理解方式 + 向量 的空间&基、坐标&坐标变换 + Eigenvalue Decompression(特征值分解) + SVD(奇异值分解, Singular Value Decomposition)

SciTech-Mathmatics - Advanced Linear Algebra(高等线性代数):

矩阵乘法 的 四种理解方式

矩阵乘法有四种理解方式：

• 线性方程组视角：将矩阵看作行向量与向量的点积。
• 列向量观点视角：将矩阵分解成列向量的线性组合。
• 向量变换视角：将矩阵看作向量的变换函数。
• 坐标变换视角：将矩阵乘法理解为同一向量在不同坐标系下的表达方式。

背景: 线性方程组 + 消元法 + 初等行变换

矩阵诞生于线性方程组的求解，最基本的运算方法来自于高斯消元法，

所以矩阵整个运算规则都符合高斯消元法，矩阵源于 线性方程组,

但经过几十年的发展已不限于求解线性方程组，可用于很多应用场景。

线性方程组如下所示：

\[\large \begin{array}{lllll} a_{11}x_1 &+a_{12}x_2 &+ \cdots & + a_{1n}x_n & = y_1 \\ a_{21}x_1 &+a_{22}x_2 &+ \cdots & + a_{2n}x_n & =y_2 \\
\cdots \\ a_{m1}x_1 &+a_{m2}x_2 & + \cdots & + a_{mn}x_n &=y_m \end{array}\]

四种视角理解

1. 线性方程组视角（向量点积视角）
   
   将线性方程组直接写成向量形式，如下所示：
   
   \(\large \begin{array}{lll} \begin{pmatrix} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n\\ \cdots \\ a_{m1}x_1+a_{m2}x_2+ \cdots +a_{mn}x_n \\ \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)

   可认为是 "矩阵的行向量" 与 "向量x" 的 点积(矩阵的行乘以向量的列)：
   
   \(\large \begin{array}{lll} \begin{pmatrix} a_{11}&a_{12}& \cdots &a_{1n}\\ a_{21}&a_{22}& \cdots &a_{2n}\\ \cdots \\ a_{m1}&a_{m2}& \cdots &a_{mn} \\ \end{pmatrix} \begin{pmatrix} x_1\\x_2\\ \cdots \\x_n \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)

2. 列向量观点视角
   
   对于\(\large Ax=y\)：
   
   \(\large \begin{array}{lll} \begin{pmatrix} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n\\ \cdots \\ a_{m1}x_1+a_{m2}x_2+ \cdots +a_{mn}x_n \\ \end{pmatrix}= \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)

   可以分解成：
   
   \(\large \begin{array}{lll} \begin{pmatrix} a_{11}\\ a_{21}\\ \cdots \\ a_{m1}\\ \end{pmatrix}x_1+\begin{pmatrix} a_{12}\\ a_{22}\\ \cdots \\ a_{m2}\\ \end{pmatrix}x_2+\begin{pmatrix} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{pmatrix}x_{ \cdots }+\begin{pmatrix} a_{1n}\\ a_{2n}\\ \cdots \\ a_{mn}\\ \end{pmatrix}x_n = \begin{pmatrix} y_1\\ y_2\\ \cdots \\ y_m \end{pmatrix} \end{array}\)

   上述就表示 向量\(\large y\) 是否能由 向量\(\large a\) 的 线性组合 得到，
   
   只要向量\(\large y\)位于向量\(\large a\)张成的向量空间，那么向量\(\large y\)一定能由向量\(\large a\)线性组合得到，
   
   即一定能找到一组\(\large x\)使得上式必然成立。

3. 向量变换视角（矩阵函数）
   
   对\(\large Ax=y\): 矩阵\(\large A\)使 向量\(\large x.\) 作 拉伸、旋转两种变换变成向量\(\large.y\)，写成函数形式:

   \[\large f(x)=Ax
   \]

   矩阵乘法 可理解为 矩阵\(\large A\) 作为一个 "线性变换函数", 将输入向量 映射到一个新向量 。
   
   对于一个 \(\large m×n\) 的矩阵 \(\large A\):

   • 定义域: 所有 n维向量的集合，即\(\large \bf{R}^n\)；
   • 值域: 可从 "矩阵乘法的列观点" 视角，值域\(\large \bf{R}^m\)。

   通过矩阵函数(在矩阵的作用下)，研究:

   • 定义域 与 值域 的 映射关系，
     
     如\(\large A\)是一个\(\large m \times n\)的矩阵，\(\large x\)是一个n维向量，
     
     那么值域可认为是由\(\large A\)的n个列向量张成的空间，
     
     张成的空间的维数等于列向量组的秩（小于等于n），即值域的维数一定是小于等于定义域的维数。
     
     通过函数视角, 可研究在矩阵\(\large A\)有什么特征下, 定义域\(\large x\)与值域\(\large y\)的关系(满/单 射特性)。
   • 矩阵函数(线性变换函数)的分解与合成:
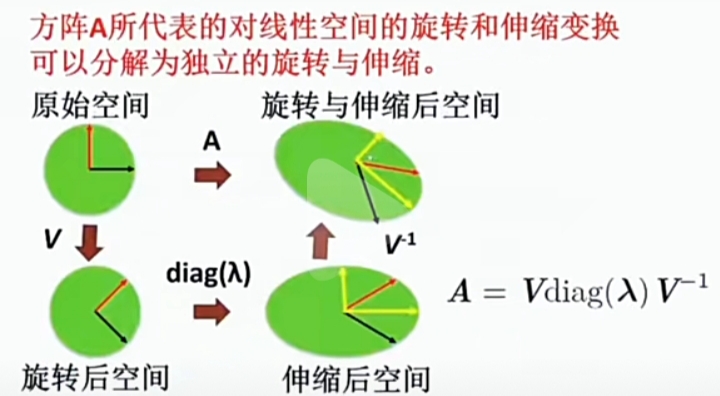
     • 任何一个"矩阵(函数)"都可分解为“伸缩与旋转”两种基本的“矩阵函数(线性变换函数)”。
     • 用“伸缩与旋转”两种基本的“矩阵函数(线性变换函数)”可合成任意目标矩阵(函数)。
     • 伸缩(基本线性变换矩阵): 特征值，
     • 旋转(基本线性变换矩阵): 等效于 “坐标系变换(换坐标系)”，

4. 坐标变换视角
   
   对于同一个向量在不同基（即为不同坐标系）下有不同的坐标值，
   
   虽然 坐标值不同, 但都表达 同一向量，即它们的方向和长度完全一致，
   
   对于 "矩阵向量的乘法", 可以认为是 "同一个向量" 在 不同的坐标系的表达，
   
   当然就可以由 "正向变换" 与 "逆向变换" 两个角度去理解矩阵乘法。

   对于\(\large Ax=y\)可以有两个坐标变换的视角，

   • 一个视角是向量\(\large x\) 自然基坐标，另外一个是非自然基坐标。
     
     对于向量\(\large x\)为非自然基坐标，向量\(\large y\)为自然基坐标，
     
     向量\(\large x\)可以理解为以矩阵\(\large A\)的列向量为基的非自然坐标系坐标，
     
     那个\(\large Ax\)运算即为将 向量\(\large x.\)转换到自然系的向量\(\large y\)的坐标。
     
     \(\large \begin{array}{lll} Ax=\begin{pmatrix} a_{11}\\ a_{21}\\ \cdots \\ a_{m1}\\ \end{pmatrix}x_1+\begin{pmatrix} a_{12}\\ a_{22}\\ \cdots \\ a_{m2}\\ \end{pmatrix}x_2+\begin{pmatrix} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \end{pmatrix}x_{ \cdots }+\begin{pmatrix} a_{1n}\\ a_{2n}\\ \cdots \\ a_{mn}\\ \end{pmatrix}x_n \\ = y_{1} e_{1} + y_{2} e_{2} + \cdots + y_{n} e_{n} \end{array}\)

   • 坐标变换的另外一个角度，是认为\(\large x\)是自然基坐标系，即：
     
     \(\large \begin{array}{lll} x=\begin{pmatrix}x_1 \\x2\\ \cdots \\x_n\end{pmatrix} = E*\begin{pmatrix}x_1 \\x2\\ \cdots \\x_n\end{pmatrix} \\ = x_1\begin{pmatrix}1\\0\\ \cdots \\0\end{pmatrix}+ x_2\begin{pmatrix}0\\1\\ \cdots \\0\end{pmatrix}+ \cdots + x_n\begin{pmatrix}0\\0\\ \cdots \\1\end{pmatrix}\\ \ \\=x_1e_1+x_2e_2+ \cdots +x_n e_n \\ = y_1 A^{-1}_{1} + y_2 A^{-1}_{2} + \cdots + y_n A^{-1}_{n} \\ A^{-1} = (A^{-1}_{1}, A^{-1}_{2}, \cdots , A^{-1}_{n}) \end{array}\)
     
     用\(\large Ax\)视角观察, 并不能直观地观察到坐标变换规律，可将其做一个简单变形：
     
     \(\large \begin{array}{lll} Ax=y\ \rightarrow \ x=A^{-1}y \end{array}\)
     
     上式的\(\large x\)是自然基坐标系，\(\large y\)是非自然基坐标系，
     
     \(\large Ax\)就将自然基坐标, 转换成以\(\large A^{-1}\)的列向量为基坐标系的坐标。
     
     矩阵向量乘法\(\large Ax=y\)，一定情况下可认为:
     
     向量\(\large x\)与向量\(\large y\)为同一向量，仅仅是坐标系不同，
     
     "一定情况下"指 "\(\large A\)为满秩矩阵"，因为 \(\large A\)为 非满秩矩阵就可能出现 "降维" 情况。

向量 的空间&基、坐标&坐标变换

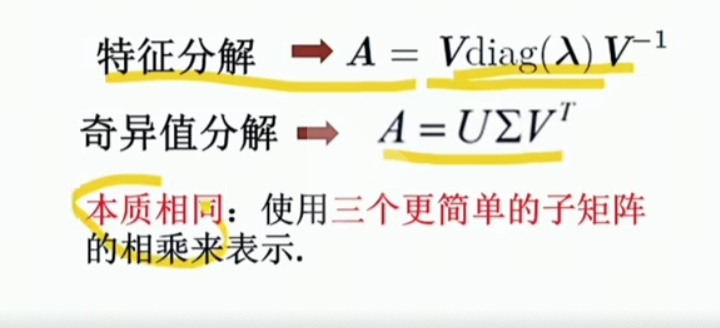
Eigenvalue Decompression(特征值分解)

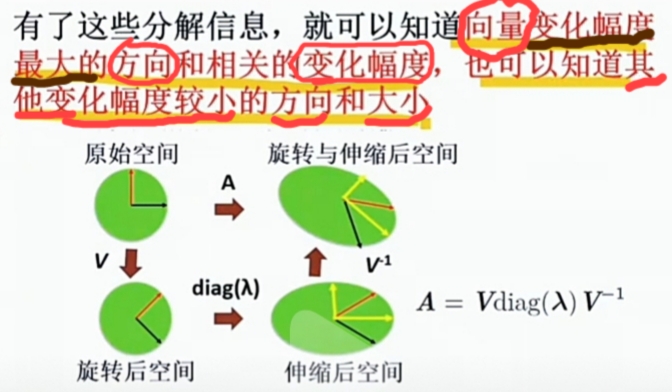
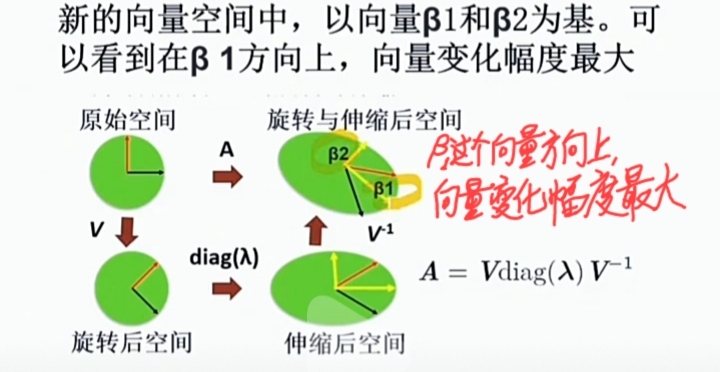
特征分解的本质之一: 利用分解结果生成新的向量空间

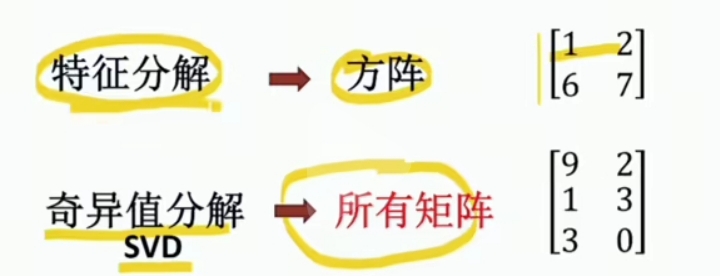
SVD(奇异值分解, Singular Value Decomposition)