双指针，BFS和图论（二）

（一）BFS

1.地牢大师

你现在被困在一个三维地牢中，需要找到最快脱离的出路！

地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。

向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。

你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。

请问，你有可能逃脱吗？

如果可以，需要多长时间？

输入格式

输入包含多组测试数据。

每组数据第一行包含三个整数 L,R,C 分别表示地牢层数，以及每一层地牢的行数和列数。

接下来是 L 个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。

每个字符用来描述一个地牢单元的具体状况。

其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。

每一个字符矩阵后面都会包含一个空行。

当输入一行为”0 0 0”时，表示输入终止。

输出格式

每组数据输出一个结果，每个结果占一行。

如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。

如果不能逃脱地牢，则输出”Trapped!”。

数据范围

1≤L,R,C≤100

输入样例：

3 4 5

S....

.###.

.##..

###.#

#####

#####

##.##

##...

#####

#####

#.###

####E

1 3 3

S##

#E#

###

0 0 0

输出样例：

Escaped in 11 minute(s).

Trapped!

解题思路：一道三维的BFS搜索题，我们可以建立三个移动数组：vx，vy，vk，分别表示北，南，东，西，上，下，设置一个三维的map数组来存储地图，
设置一个vis数组，用来判断是否走过以及距离。
代码：

#include<iostream>

#include<queue>

#include<cstring>

using namespace std;

const int N=;

int l,r,c;

char map[N][N][N];

int vis[N][N][N];

int vx[]={,-,,,,};

int vy[]={,,,-,,};

int vk[]={,,,,,-};

typedef struct Node

{

    int k,x,y;

};

bool check(int K,int X,int Y)

{

    if(X<||X>=r||Y<||Y>=c||K<||K>=l)

        return false;

    if(map[K][X][Y]=='#')

        return false;

    if(vis[K][X][Y]!=)

        return false;

    return true;

}

int bfs(Node start)

{

    queue<Node> q;

    memset(vis,,sizeof(vis));

    q.push(start);

    while(!q.empty())

    {

        Node tem=q.front();

        if(map[tem.k][tem.x][tem.y]=='E')

            return vis[tem.k][tem.x][tem.y];

        q.pop();

        for(int i=;i<;i++)

        {

            int X=tem.x+vx[i];

            int Y=tem.y+vy[i];

            int K=tem.k+vk[i];

            if(check(K,X,Y)==false)

                continue;

            vis[K][X][Y]=vis[tem.k][tem.x][tem.y]+;

            Node t={K,X,Y};

            q.push(t);

        }

    }

    return ;

}

int main()

{

    int i,j,bx,by,bk,k;

    Node start;

    string ss;

    while()

    {

        cin>>l>>r>>c;

        if(l==&&r==&&c==)

            break;

        for(k=;k<l;k++)

        {

            for(i=;i<r;i++)

            {

                for(j=;j<c;j++)

                {

                    cin>>map[k][i][j];

                    if(map[k][i][j]=='S')

                    {

                        bk=k,bx=i,by=j;

                        start={bk,bx,by};

                    }

                }

            }

            getline(cin,ss);

        }

    int ans=bfs(start);

    if(ans)

        cout<<"Escaped in "<<ans<<" minute(s)."<<endl;

    else

        cout<<"Trapped!"<<endl;

    }

    return ;

}

2.全球变暖

你有一张某海域 N×N 像素的照片，”.”表示海洋、”#”表示陆地，如下所示：

.......

.##....

.##....

....##.

..####.

...###.

.......

其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿，例如上图就有 2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。

具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......

.......

.......

.......

....#..

.......

.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入格式

第一行包含一个整数N。

以下 N 行 N 列，包含一个由字符”#”和”.”构成的 N×N 字符矩阵，代表一张海域照片，”#”表示陆地，”.”表示海洋。

照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

输出格式

一个整数表示答案。

数据范围

1≤N≤1000

输入样例1：

7

.......

.##....

.##....

....##.

..####.

...###.

.......

输出样例1：

输入样例2：

9

.........

.##.##...

.#####...

.##.##...

.........

.##.#....

.#.###...

.#..#....

.........

输出样例2：

解题思路：该题要找出完全被淹没的岛屿的个数，首先我们要做的是找出所有的联通快，我们可以用bfs来找，对于每一个联通快我们需要判断他是否被完全淹没，如何判断呢？

我们可以找出该联通块里一共有多少个像素，再找出有多少个像素与海相邻，如果两者的个数相等，那么该岛屿必然会被完全淹没。

否则，不会完全淹没。特别注意：当你用bfs开始寻找时，此时的像素总数的初始值为1.

代码：

#include<iostream>

#include<cstring>

#include<queue>

#include<cstdio>

using namespace std;

const int N=;

char map[N][N];

bool ts[N][N];

int vx[]={,-,,};

int vy[]={,,,-};

int ans,n;

typedef struct Node

{

    int x,y;

};

bool check(int X,int Y)

{

    if(X<||X>=n||Y<||Y>=n)

        return false;

    if(map[X][Y]=='.')

        return false;

    if(ts[X][Y]==true)

        return false;

    return true;

}

void bfs(int i,int j)

{

    Node start={i,j};

    queue<Node> q;

    ts[i][j]=true;

    q.push(start);

    int total=,ver=;

    while(q.size())

    {

        Node t=q.front();

        q.pop();

        int flag=false;

        for(i=;i<;i++)

        {

            int X=t.x+vx[i];

            int Y=t.y+vy[i];

            if(X>=&&X<n&&Y>=&&Y<n&&map[X][Y]=='.')

            {

                flag=true;

            }

            if(check(X,Y)==false)

                continue;

            total++;

            ts[X][Y]=true;

            Node f={X,Y};

            q.push(f);

        }

        if(flag)

            ver++;

    }

    if(total==ver)

        ans++;

}

int main()

{

    int i,j;

    cin>>n;

    for(i=;i<n;i++)

    {

        for(j=;j<n;j++)

        {

            cin>>map[i][j];

        }

    }

    for(i=;i<n;i++)

    {

        for(j=;j<n;j++)

        {

            if(!ts[i][j]&&map[i][j]=='#')

            {

                bfs(i,j);

            }

        }

    }

    cout<<ans;

    return ;

}

3.完全二叉树的权值

给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1,A2,⋅⋅⋅AN，如下图所示：

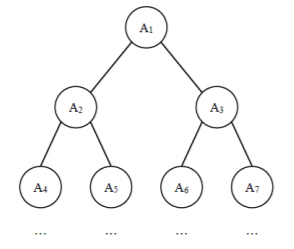
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？

如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入格式

第一行包含一个整数 N。

第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。

输出格式

输出一个整数代表答案。

数据范围

1≤N≤10⁵,
−10⁵≤Ai≤10⁵

输入样例：

7

1 6 5 4 3 2 1

输出样例：

解题思路：每一层的个数都是=2^n-1个，而且开头的下标都是2的倍数
代码：

#include<iostream>

using namespace std;

const int N=;

typedef long long ll;

ll a[N];

ll maxn,sum,ans;

int main()

{

    ll i,j,n,k;

    cin>>n;

    for(i=;i<=n;i++)

        cin>>a[i];

    maxn=a[];

    ans=;

    k=;

    for(i=;i<=n;i=i*)

    {

        sum=;

        for(j=i;j<=i*-&&j<=n;j++)

        {

            sum+=a[j];

        }

        k++;

        if(sum>maxn)

        {

            maxn=sum;

            ans=k;

        }

    }

    cout<<ans;

    return ;

}